Question Number 148835 by DELETED last updated on 31/Jul/21
Answered by DELETED last updated on 31/Jul/21

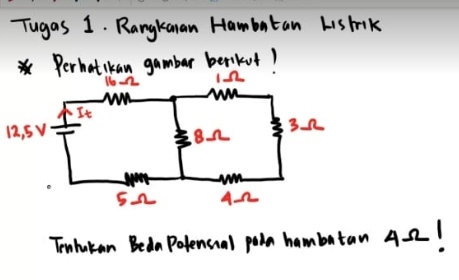
$$\mathrm{Lihat}\:\mathrm{Hambatan}\:\mathrm{Seri}\:\mathrm{satu} \\ $$$$\mathrm{R}_{\mathrm{s1}} =\mathrm{R}_{\mathrm{1}\Omega} +\mathrm{R}_{\mathrm{3}\Omega} +\mathrm{R}_{\mathrm{4}\Omega} \\ $$$$\mathrm{R}_{\mathrm{s1}} =\mathrm{1}+\mathrm{3}+\mathrm{4}=\mathrm{8}\:\Omega \\ $$$$\mathrm{Lihat}\:\mathrm{Hambatan}\:\mathrm{Paralel} \\ $$$$\frac{\mathrm{1}}{\mathrm{R}_{\mathrm{p}} }\:=\:\frac{\mathrm{1}}{\mathrm{R}_{\mathrm{s1}} }\:+\:\frac{\mathrm{1}}{\mathrm{R}_{\mathrm{8}\Omega} }\:=\:\frac{\mathrm{1}}{\mathrm{8}}+\frac{\mathrm{1}}{\mathrm{8}}\:=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{R}_{\mathrm{p}} =\mathrm{4}\:\Omega \\ $$$$\mathrm{Lihat}\:\mathrm{Hambatan}\:\mathrm{Seri}\:\mathrm{dua} \\ $$$$\mathrm{R}_{\mathrm{total}} =\mathrm{R}_{\mathrm{s2}} =\mathrm{R}_{\mathrm{16}\Omega} +\mathrm{R}_{\mathrm{5}\Omega} +\mathrm{R}_{\mathrm{p}} \\ $$$$\:\:\:\:\:\:\:=\mathrm{16}+\mathrm{5}+\mathrm{4}=\mathrm{25}\Omega \\ $$$$\mathrm{i}_{\mathrm{total}} =\frac{\mathrm{V}}{\mathrm{R}_{\mathrm{total}} }\:=\frac{\mathrm{12}.\mathrm{5}}{\mathrm{25}}\:=\mathrm{0}.\mathrm{5}\:\mathrm{A} \\ $$$$\mathrm{i}_{\mathrm{total}\:} =\mathrm{i}_{\mathrm{p}} =\mathrm{0}.\mathrm{5}\:\mathrm{A} \\ $$$$\mathrm{V}_{\mathrm{p}} =\mathrm{i}_{\mathrm{p}} ×\mathrm{R}_{\mathrm{p}} =\mathrm{0}.\mathrm{5}×\mathrm{4}=\mathrm{2}\:\mathrm{V} \\ $$$$\mathrm{V}_{\mathrm{p}} =\mathrm{V}_{\mathrm{s1}} \:=\mathrm{2}\:\mathrm{V} \\ $$$$\mathrm{i}_{\mathrm{s1}} =\frac{\mathrm{V}_{\mathrm{s1}} }{\mathrm{R}_{\mathrm{s1}} }\:=\:\frac{\mathrm{2}}{\mathrm{8}}=\mathrm{0}.\mathrm{25}\:\mathrm{A} \\ $$$$\mathrm{i}_{\mathrm{s1}} =\mathrm{i}_{\mathrm{4}\Omega} =\mathrm{0}.\mathrm{25}\:\mathrm{A}// \\ $$
Commented by DELETED last updated on 01/Aug/21

