Question Number 148884 by 0731619 last updated on 01/Aug/21
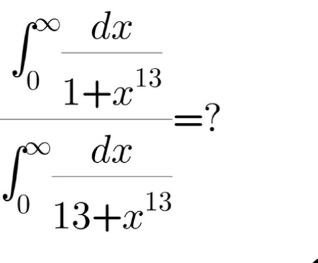
Answered by aleks041103 last updated on 03/Aug/21

$$\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{{a}+{x}^{\mathrm{13}} }=\frac{\mathrm{1}}{{a}}\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\mathrm{1}+\left(\frac{{x}}{{a}^{\mathrm{1}/\mathrm{13}} }\right)^{\mathrm{13}} }= \\ $$$$=\frac{{a}^{\mathrm{1}/\mathrm{13}} }{{a}}\int_{\mathrm{0}} ^{\infty} \frac{{d}\left({x}/{a}^{\mathrm{1}/\mathrm{13}} \right)}{\mathrm{1}+\left({x}/{a}^{\mathrm{1}/\mathrm{13}} \right)^{\mathrm{13}} } \\ $$$${if}\:{a}>\mathrm{0},\:{then}\:{we}\:{substitute}\: \\ $$$${u}={x}/{a}^{\mathrm{1}/\mathrm{13}} \\ $$$${Then}: \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{{a}+{x}^{\mathrm{13}} }={a}^{−\mathrm{12}/\mathrm{13}} \int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\mathrm{1}+{x}^{\mathrm{13}} } \\ $$$$\Rightarrow\frac{\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\mathrm{1}+{x}^{\mathrm{13}} }}{\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\mathrm{13}+{x}^{\mathrm{13}} }}=\mathrm{13}^{\mathrm{12}/\mathrm{13}} \\ $$
