Question Number 148886 by DELETED last updated on 01/Aug/21
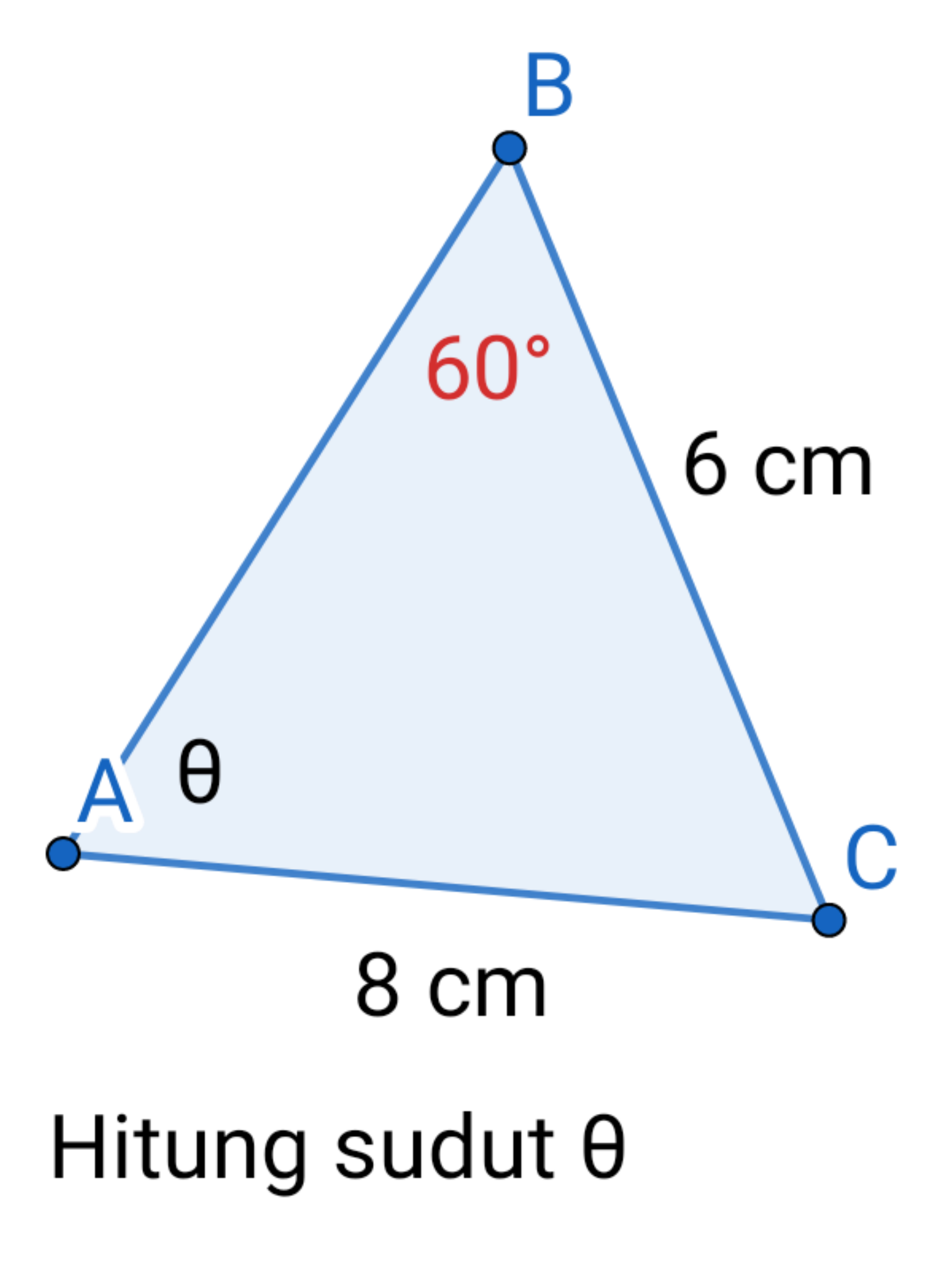
Answered by Rasheed.Sindhi last updated on 01/Aug/21
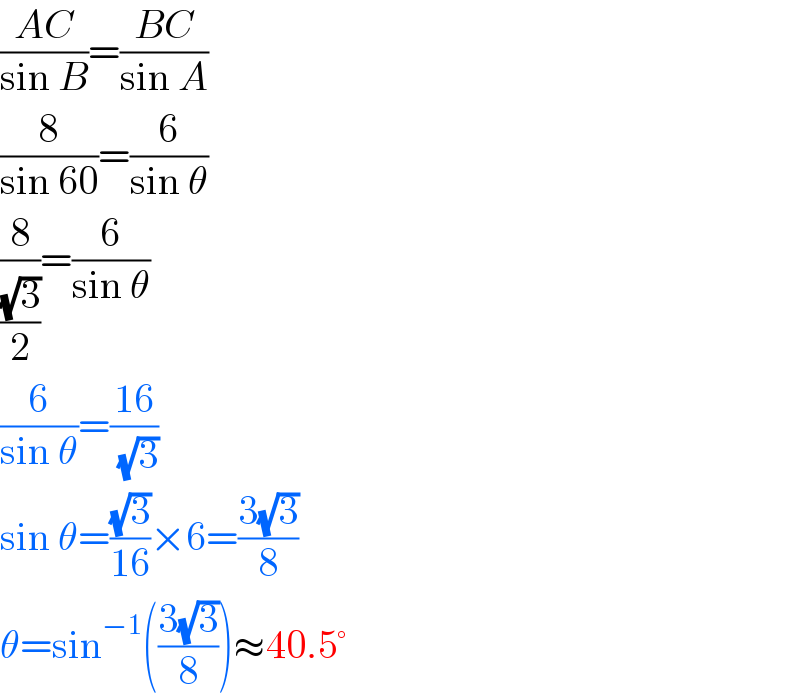
$$\frac{{AC}}{\mathrm{sin}\:{B}}=\frac{{BC}}{\mathrm{sin}\:{A}} \\ $$$$\frac{\mathrm{8}}{\mathrm{sin}\:\mathrm{60}}=\frac{\mathrm{6}}{\mathrm{sin}\:\theta} \\ $$$$\frac{\mathrm{8}}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}=\frac{\mathrm{6}}{\mathrm{sin}\:\theta} \\ $$$$\frac{\mathrm{6}}{\mathrm{sin}\:\theta}=\frac{\mathrm{16}}{\:\sqrt{\mathrm{3}}} \\ $$$$\mathrm{sin}\:\theta=\frac{\sqrt{\mathrm{3}}}{\mathrm{16}}×\mathrm{6}=\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{8}} \\ $$$$\theta=\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{8}}\right)\approx\mathrm{40}.\mathrm{5}° \\ $$
