Question-149008

Question Number 149008 by Samimsultani last updated on 02/Aug/21

Commented by bramlexs22 last updated on 02/Aug/21

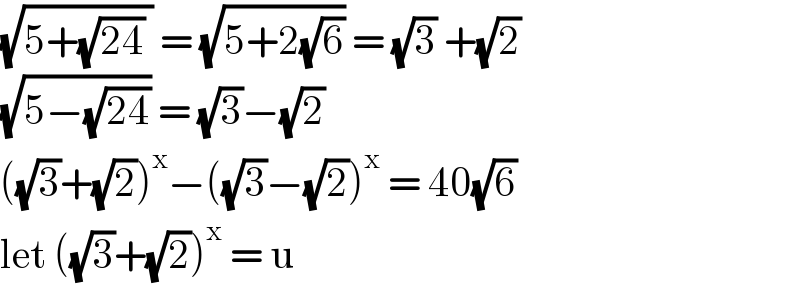
(√(5+(√(24)) )) = (√(5+2(√6))) = (√3) +(√2) (√(5−(√(24)))) = (√3)−(√2) ((√3)+(√2))^x −((√3)−(√2))^x = 40(√6) let ((√3)+(√2))^x = u

$$\sqrt{\mathrm{5}+\sqrt{\mathrm{24}}\:}\:=\:\sqrt{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}}\:=\:\sqrt{\mathrm{3}}\:+\sqrt{\mathrm{2}}\: \\ $$$$\sqrt{\mathrm{5}−\sqrt{\mathrm{24}}}\:=\:\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}} \\ $$$$\left(\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}\right)^{\mathrm{x}} −\left(\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}\right)^{\mathrm{x}} \:=\:\mathrm{40}\sqrt{\mathrm{6}} \\ $$$$\mathrm{let}\:\left(\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}\right)^{\mathrm{x}} \:=\:\mathrm{u} \\ $$

Commented by Samimsultani last updated on 02/Aug/21

$$???? \\ $$

Commented by bramlexs22 last updated on 02/Aug/21

$$\mathrm{you}\:\mathrm{can}\:\mathrm{finish}\:\mathrm{it} \\ $$

Answered by Rasheed.Sindhi last updated on 02/Aug/21

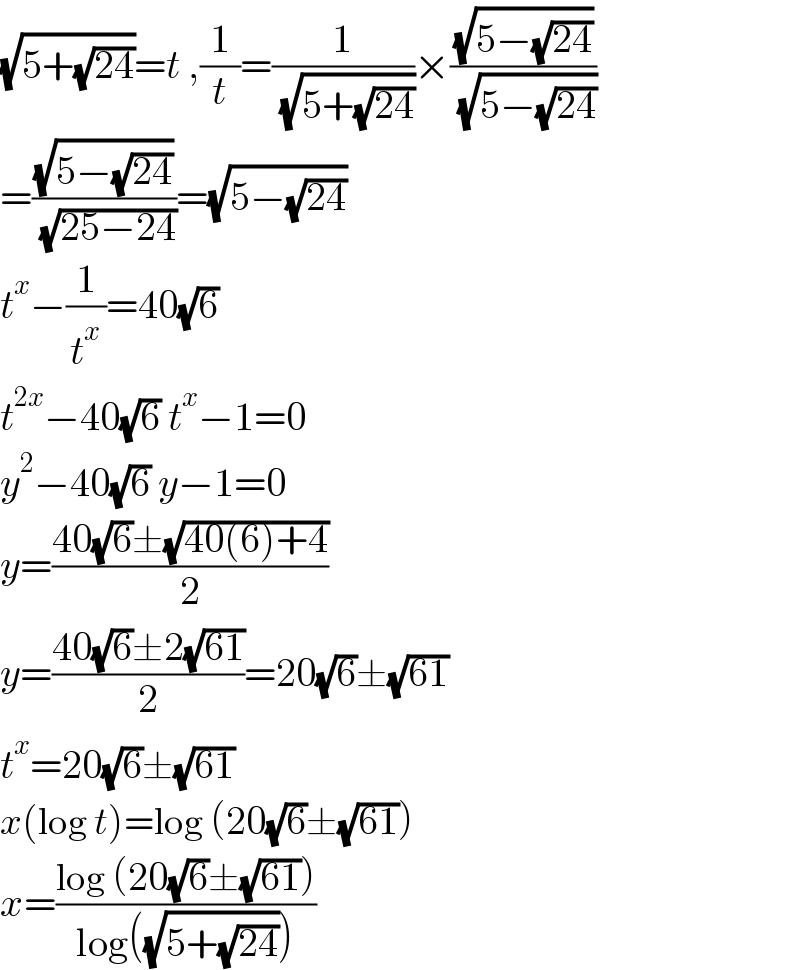
(√(5+(√(24))))=t ,(1/t)=(1/( (√(5+(√(24))))))×((√(5−(√(24))))/( (√(5−(√(24)))))) =((√(5−(√(24))))/( (√(25−24))))=(√(5−(√(24)))) t^x −(1/t^x )=40(√6) t^(2x) −40(√6) t^x −1=0 y^2 −40(√6) y−1=0 y=((40(√6)±(√(40(6)+4)))/2) y=((40(√6)±2(√(61)))/2)=20(√6)±(√(61)) t^x =20(√6)±(√(61)) x(log t)=log (20(√6)±(√(61))) x=((log (20(√6)±(√(61))))/(log((√(5+(√(24)))))))

$$\sqrt{\mathrm{5}+\sqrt{\mathrm{24}}}={t}\:,\frac{\mathrm{1}}{{t}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}+\sqrt{\mathrm{24}}}}×\frac{\sqrt{\mathrm{5}−\sqrt{\mathrm{24}}}}{\:\sqrt{\mathrm{5}−\sqrt{\mathrm{24}}}} \\ $$$$=\frac{\sqrt{\mathrm{5}−\sqrt{\mathrm{24}}}}{\:\sqrt{\mathrm{25}−\mathrm{24}}}=\sqrt{\mathrm{5}−\sqrt{\mathrm{24}}} \\ $$$${t}^{{x}} −\frac{\mathrm{1}}{{t}^{{x}} }=\mathrm{40}\sqrt{\mathrm{6}} \\ $$$${t}^{\mathrm{2}{x}} −\mathrm{40}\sqrt{\mathrm{6}}\:{t}^{{x}} −\mathrm{1}=\mathrm{0} \\ $$$${y}^{\mathrm{2}} −\mathrm{40}\sqrt{\mathrm{6}}\:{y}−\mathrm{1}=\mathrm{0} \\ $$$${y}=\frac{\mathrm{40}\sqrt{\mathrm{6}}\pm\sqrt{\mathrm{40}\left(\mathrm{6}\right)+\mathrm{4}}}{\mathrm{2}} \\ $$$${y}=\frac{\mathrm{40}\sqrt{\mathrm{6}}\pm\mathrm{2}\sqrt{\mathrm{61}}}{\mathrm{2}}=\mathrm{20}\sqrt{\mathrm{6}}\pm\sqrt{\mathrm{61}} \\ $$$${t}^{{x}} =\mathrm{20}\sqrt{\mathrm{6}}\pm\sqrt{\mathrm{61}} \\ $$$${x}\left(\mathrm{log}\:{t}\right)=\mathrm{log}\:\left(\mathrm{20}\sqrt{\mathrm{6}}\pm\sqrt{\mathrm{61}}\right) \\ $$$${x}=\frac{\mathrm{log}\:\left(\mathrm{20}\sqrt{\mathrm{6}}\pm\sqrt{\mathrm{61}}\right)}{\mathrm{log}\left(\sqrt{\mathrm{5}+\sqrt{\mathrm{24}}}\right)} \\ $$

Answered by mr W last updated on 02/Aug/21

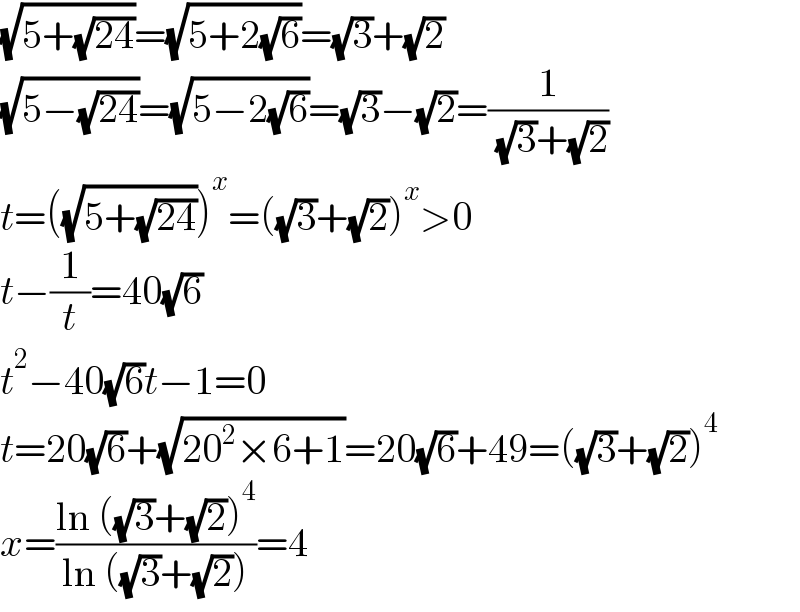
(√(5+(√(24))))=(√(5+2(√6)))=(√3)+(√2) (√(5−(√(24))))=(√(5−2(√6)))=(√3)−(√2)=(1/( (√3)+(√2))) t=((√(5+(√(24)))))^x =((√3)+(√2))^x >0 t−(1/t)=40(√6) t^2 −40(√6)t−1=0 t=20(√6)+(√(20^2 ×6+1))=20(√6)+49=((√3)+(√2))^4 x=((ln ((√3)+(√2))^4 )/(ln ((√3)+(√2))))=4

$$\sqrt{\mathrm{5}+\sqrt{\mathrm{24}}}=\sqrt{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}}=\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}} \\ $$$$\sqrt{\mathrm{5}−\sqrt{\mathrm{24}}}=\sqrt{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}}}=\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}} \\ $$$${t}=\left(\sqrt{\mathrm{5}+\sqrt{\mathrm{24}}}\right)^{{x}} =\left(\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}\right)^{{x}} >\mathrm{0} \\ $$$${t}−\frac{\mathrm{1}}{{t}}=\mathrm{40}\sqrt{\mathrm{6}} \\ $$$${t}^{\mathrm{2}} −\mathrm{40}\sqrt{\mathrm{6}}{t}−\mathrm{1}=\mathrm{0} \\ $$$${t}=\mathrm{20}\sqrt{\mathrm{6}}+\sqrt{\mathrm{20}^{\mathrm{2}} ×\mathrm{6}+\mathrm{1}}=\mathrm{20}\sqrt{\mathrm{6}}+\mathrm{49}=\left(\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}\right)^{\mathrm{4}} \\ $$$${x}=\frac{\mathrm{ln}\:\left(\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}\right)^{\mathrm{4}} }{\mathrm{ln}\:\left(\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}\right)}=\mathrm{4} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply