Question-149081

Question Number 149081 by Integrals last updated on 02/Aug/21

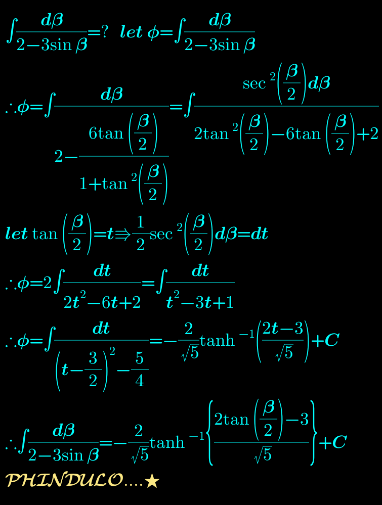
Answered by Ar Brandon last updated on 02/Aug/21

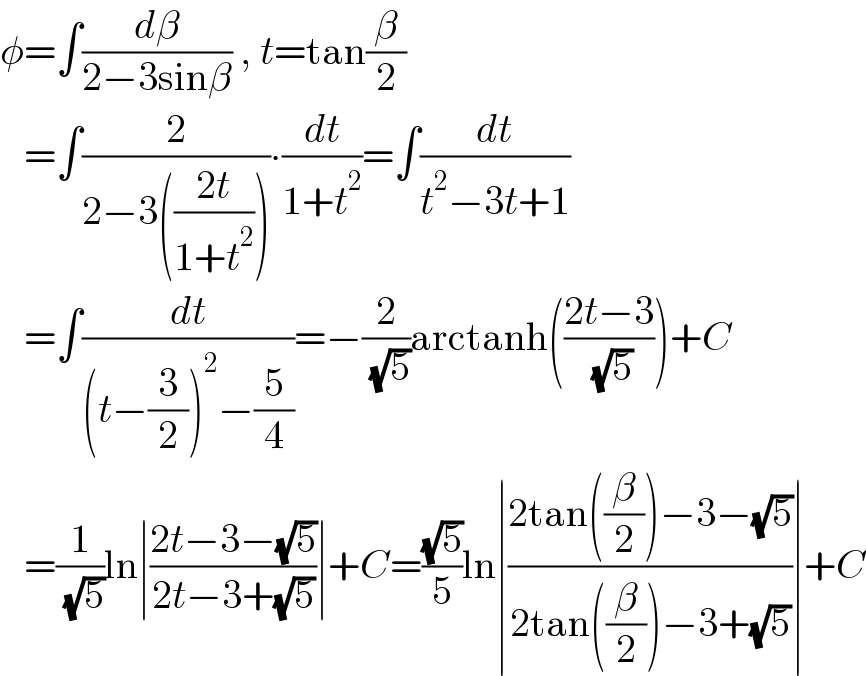
φ=∫(dβ/(2−3sinβ)) , t=tan(β/2) =∫(2/(2−3(((2t)/(1+t^2 )))))∙(dt/(1+t^2 ))=∫(dt/(t^2 −3t+1)) =∫(dt/((t−(3/2))^2 −(5/4)))=−(2/( (√5)))arctanh(((2t−3)/( (√5))))+C =(1/( (√5)))ln∣((2t−3−(√5))/(2t−3+(√5)))∣+C=((√5)/5)ln∣((2tan((β/2))−3−(√5))/(2tan((β/2))−3+(√5)))∣+C

$$\phi=\int\frac{{d}\beta}{\mathrm{2}−\mathrm{3sin}\beta}\:,\:{t}=\mathrm{tan}\frac{\beta}{\mathrm{2}} \\ $$$$\:\:\:=\int\frac{\mathrm{2}}{\mathrm{2}−\mathrm{3}\left(\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\right)}\centerdot\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }=\int\frac{{dt}}{{t}^{\mathrm{2}} −\mathrm{3}{t}+\mathrm{1}} \\ $$$$\:\:\:=\int\frac{{dt}}{\left({t}−\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{5}}{\mathrm{4}}}=−\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\mathrm{arctanh}\left(\frac{\mathrm{2}{t}−\mathrm{3}}{\:\sqrt{\mathrm{5}}}\right)+{C} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\mathrm{ln}\mid\frac{\mathrm{2}{t}−\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{2}{t}−\mathrm{3}+\sqrt{\mathrm{5}}}\mid+{C}=\frac{\sqrt{\mathrm{5}}}{\mathrm{5}}\mathrm{ln}\mid\frac{\mathrm{2tan}\left(\frac{\beta}{\mathrm{2}}\right)−\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{2tan}\left(\frac{\beta}{\mathrm{2}}\right)−\mathrm{3}+\sqrt{\mathrm{5}}}\mid+{C} \\ $$

Commented by Ar Brandon last updated on 02/Aug/21

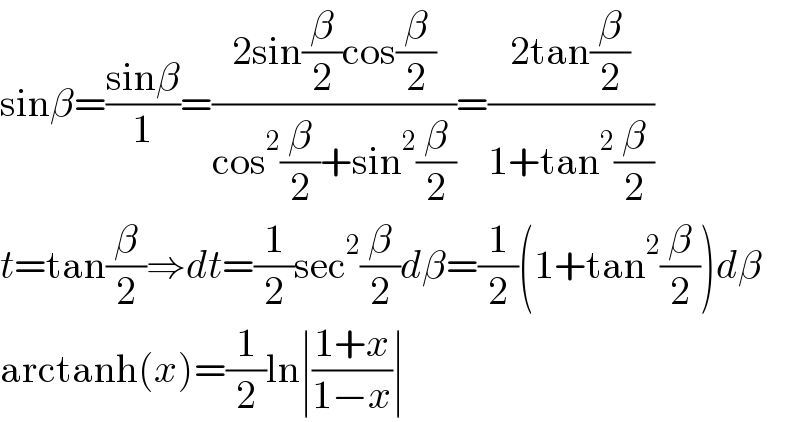
sinβ=((sinβ)/1)=((2sin(β/2)cos(β/2))/(cos^2 (β/2)+sin^2 (β/2)))=((2tan(β/2))/(1+tan^2 (β/2))) t=tan(β/2)⇒dt=(1/2)sec^2 (β/2)dβ=(1/2)(1+tan^2 (β/2))dβ arctanh(x)=(1/2)ln∣((1+x)/(1−x))∣

$$\mathrm{sin}\beta=\frac{\mathrm{sin}\beta}{\mathrm{1}}=\frac{\mathrm{2sin}\frac{\beta}{\mathrm{2}}\mathrm{cos}\frac{\beta}{\mathrm{2}}}{\mathrm{cos}^{\mathrm{2}} \frac{\beta}{\mathrm{2}}+\mathrm{sin}^{\mathrm{2}} \frac{\beta}{\mathrm{2}}}=\frac{\mathrm{2tan}\frac{\beta}{\mathrm{2}}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \frac{\beta}{\mathrm{2}}} \\ $$$${t}=\mathrm{tan}\frac{\beta}{\mathrm{2}}\Rightarrow{dt}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sec}^{\mathrm{2}} \frac{\beta}{\mathrm{2}}{d}\beta=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \frac{\beta}{\mathrm{2}}\right){d}\beta \\ $$$$\mathrm{arctanh}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\mid \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply