Question Number 149180 by mathdanisur last updated on 03/Aug/21

Answered by Kamel last updated on 03/Aug/21
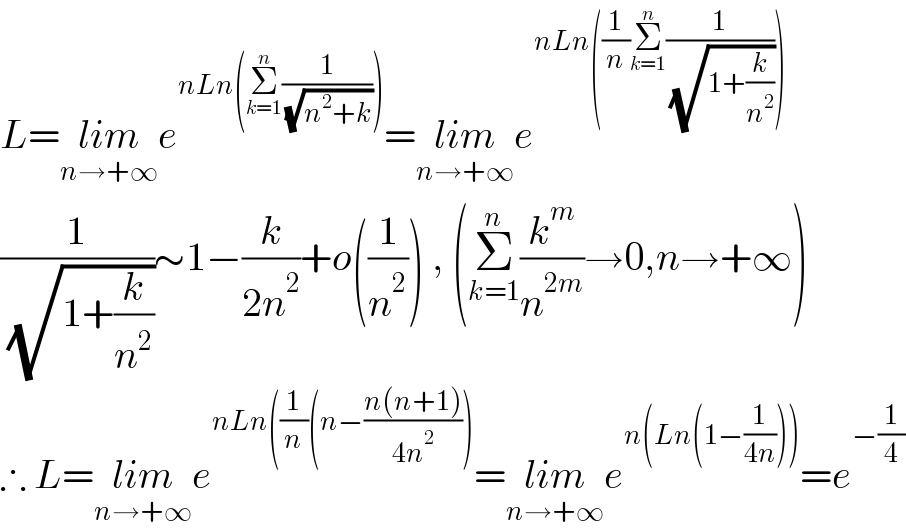
$${L}=\underset{{n}\rightarrow+\infty} {{lim}e}^{{nLn}\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\:\sqrt{{n}^{\mathrm{2}} +{k}}}\right)} =\underset{{n}\rightarrow+\infty} {{lim}e}^{{nLn}\left(\frac{\mathrm{1}}{{n}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\frac{{k}}{{n}^{\mathrm{2}} }}}\right)} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\frac{{k}}{{n}^{\mathrm{2}} }}}\sim\mathrm{1}−\frac{{k}}{\mathrm{2}{n}^{\mathrm{2}} }+{o}\left(\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)\:,\:\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{k}^{{m}} }{{n}^{\mathrm{2}{m}} }\rightarrow\mathrm{0},{n}\rightarrow+\infty\right) \\ $$$$\therefore\:{L}=\underset{{n}\rightarrow+\infty} {{lim}e}^{{nLn}\left(\frac{\mathrm{1}}{{n}}\left({n}−\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{4}{n}^{\mathrm{2}} }\right)\right.} =\underset{{n}\rightarrow+\infty} {{lim}e}^{{n}\left({Ln}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}{n}}\right)\right)} ={e}^{−\frac{\mathrm{1}}{\mathrm{4}}} \\ $$
Commented by mathdanisur last updated on 03/Aug/21

$${Thank}\:{You}\:{Ser} \\ $$
