Question Number 149189 by Naser last updated on 03/Aug/21
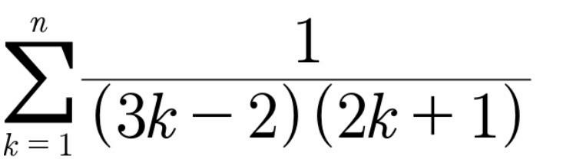
Commented by Tawa11 last updated on 03/Aug/21

$$\mathrm{great} \\ $$
Answered by Ar Brandon last updated on 03/Aug/21
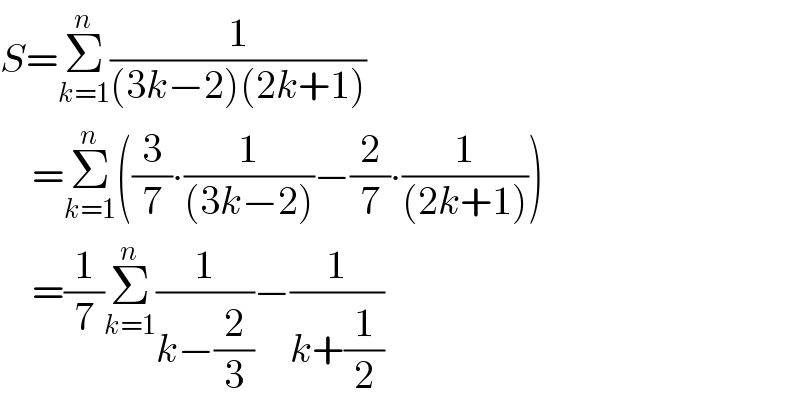
$${S}=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{3}{k}−\mathrm{2}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)} \\ $$$$\:\:\:\:=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\frac{\mathrm{3}}{\mathrm{7}}\centerdot\frac{\mathrm{1}}{\left(\mathrm{3}{k}−\mathrm{2}\right)}−\frac{\mathrm{2}}{\mathrm{7}}\centerdot\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{1}\right)}\right) \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{7}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{k}−\frac{\mathrm{2}}{\mathrm{3}}}−\frac{\mathrm{1}}{{k}+\frac{\mathrm{1}}{\mathrm{2}}} \\ $$
Answered by nimnim last updated on 03/Aug/21

$${Let}\:{me}\:{give}\:{a}\:{try}. \\ $$$${S}=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{3}{k}−\mathrm{2}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)} \\ $$$$\:\:\:=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\frac{\mathrm{3}}{\mathrm{7}}.\frac{\mathrm{1}}{\mathrm{3}{k}−\mathrm{2}}−\frac{\mathrm{2}}{\mathrm{7}}.\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{1}}\right) \\ $$$$\:\:\:=\frac{\mathrm{3}}{\mathrm{7}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\:\frac{\mathrm{1}}{\left(\mathrm{3}{k}−\mathrm{2}\right)}−\frac{\mathrm{2}}{\mathrm{7}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{1}\right)} \\ $$$$\:\:\:=\frac{\mathrm{3}}{\mathrm{7}}\left(\frac{\mathrm{1}}{\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{7}}+….+\frac{\mathrm{1}}{\mathrm{1}+\left({n}−\mathrm{1}\right).\mathrm{3}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:−\frac{\mathrm{2}}{\mathrm{7}}\left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{7}}+…+\frac{\mathrm{1}}{\mathrm{3}+\left({n}−\mathrm{1}\right).\mathrm{2}}\right) \\ $$$$\:\:\:\:\:{both}\:{are}\:{harmonic}\:{progression}\:{to}\:{n}\:{terms} \\ $$$$\:\:\:\:\:\:{S}=\frac{\mathrm{1}}{{d}}{ln}\mid\left(\frac{\mathrm{2}{a}+\left(\mathrm{2}{n}−\mathrm{1}\right){d}}{\mathrm{2}{a}−{d}}\right)\mid \\ $$$$\therefore{S}=\frac{\mathrm{3}}{\mathrm{7}}×\frac{\mathrm{1}}{\mathrm{3}}{ln}\mid\left(\frac{\mathrm{2}.\mathrm{1}+\left(\mathrm{2}{n}−\mathrm{1}\right).\mathrm{3}}{\mathrm{2}.\mathrm{1}−\mathrm{3}}\right)\mid−\frac{\mathrm{2}}{\mathrm{7}}×\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\left(\frac{\mathrm{2}.\mathrm{3}+\left(\mathrm{2}{n}−\mathrm{1}\right).\mathrm{2}}{\mathrm{2}.\mathrm{3}−\mathrm{2}}\right)\mid \\ $$$$\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{7}}{ln}\mid\frac{\mathrm{2}{n}−\mathrm{1}}{−\mathrm{1}}\mid−\frac{\mathrm{1}}{\mathrm{7}}{ln}\mid\frac{\mathrm{4}+\mathrm{4}{n}}{\mathrm{4}}\mid \\ $$$$\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{7}}\left({ln}\mid\mathrm{1}−\mathrm{2}{n}\mid−{ln}\mid\mathrm{1}+{n}\mid\right) \\ $$$$\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{7}}{ln}\mid\frac{\mathrm{1}−\mathrm{2}{n}}{\mathrm{1}+{n}}\mid \\ $$$$\:\:\:\:\:\: \\ $$
