Question-149268

Question Number 149268 by Samimsultani last updated on 04/Aug/21

Answered by dkenechukwu04 last updated on 04/Aug/21

Let 2+(3/(2+(3/(2+(3/(2+...))))))=x 5+(2/x)=5+(2/(2+(3/x))) 5+(2/x)=5+((2x)/(2x+3)) ((5x+2)/x)=((12x+15)/(2x+3)) 10x^2 +19x+6=12x^2 +15x 2x^2 −4x−6=0 x^2 −2x−3=0 (x−3)(x+1)=0 ∴x=3; x=-1 when x=3 5+(2/x)=5+(2/3) =5.67 when x=-1 5+(2/x)=5+(2/(-1)) =3

$$\mathrm{Let}\:\mathrm{2}+\frac{\mathrm{3}}{\mathrm{2}+\frac{\mathrm{3}}{\mathrm{2}+\frac{\mathrm{3}}{\mathrm{2}+…}}}={x} \\ $$$$\mathrm{5}+\frac{\mathrm{2}}{{x}}=\mathrm{5}+\frac{\mathrm{2}}{\mathrm{2}+\frac{\mathrm{3}}{{x}}} \\ $$$$\mathrm{5}+\frac{\mathrm{2}}{{x}}=\mathrm{5}+\frac{\mathrm{2}{x}}{\mathrm{2}{x}+\mathrm{3}} \\ $$$$\frac{\mathrm{5}{x}+\mathrm{2}}{{x}}=\frac{\mathrm{12}{x}+\mathrm{15}}{\mathrm{2}{x}+\mathrm{3}} \\ $$$$\mathrm{10}{x}^{\mathrm{2}} +\mathrm{19}{x}+\mathrm{6}=\mathrm{12}{x}^{\mathrm{2}} +\mathrm{15}{x} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} −\mathrm{4}{x}−\mathrm{6}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{3}=\mathrm{0} \\ $$$$\left({x}−\mathrm{3}\right)\left({x}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\therefore{x}=\mathrm{3};\:{x}=-\mathrm{1} \\ $$$$\mathrm{when}\:{x}=\mathrm{3} \\ $$$$\mathrm{5}+\frac{\mathrm{2}}{{x}}=\mathrm{5}+\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\mathrm{5}.\mathrm{67} \\ $$$$\mathrm{when}\:{x}=-\mathrm{1} \\ $$$$\mathrm{5}+\frac{\mathrm{2}}{{x}}=\mathrm{5}+\frac{\mathrm{2}}{-\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{3} \\ $$$$ \\ $$

Answered by nimnim last updated on 04/Aug/21

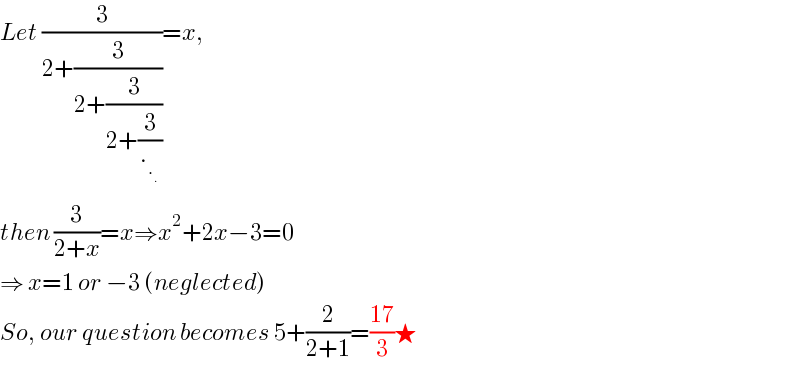
Let (3/(2+(3/(2+(3/(2+(3/._._. )))))))=x, then (3/(2+x))=x⇒x^2 +2x−3=0 ⇒ x=1 or −3 (neglected) So, our question becomes 5+(2/(2+1))=((17)/3)★

$${Let}\:\frac{\mathrm{3}}{\mathrm{2}+\frac{\mathrm{3}}{\mathrm{2}+\frac{\mathrm{3}}{\mathrm{2}+\frac{\mathrm{3}}{._{._{.} } }}}}={x},\: \\ $$$${then}\:\frac{\mathrm{3}}{\mathrm{2}+{x}}={x}\Rightarrow{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{3}=\mathrm{0} \\ $$$$\Rightarrow\:{x}=\mathrm{1}\:{or}\:−\mathrm{3}\:\left({neglected}\right) \\ $$$${So},\:{our}\:{question}\:{becomes}\:\mathrm{5}+\frac{\mathrm{2}}{\mathrm{2}+\mathrm{1}}=\frac{\mathrm{17}}{\mathrm{3}}\bigstar \\ $$

Answered by john_santu last updated on 04/Aug/21

let 2+(3/(2+(3/(2+(3/⋮))))) = x ⇒x = 2+(3/x) ; x^2 −2x−3=0 ⇒(x−3)(x+1)=0 ⇒x = 3 or x=−1(rejected) then 5 +(2/x) = 5+(2/3)=((17)/3)

$$\mathrm{let}\:\mathrm{2}+\frac{\mathrm{3}}{\mathrm{2}+\frac{\mathrm{3}}{\mathrm{2}+\frac{\mathrm{3}}{\vdots}}}\:=\:\mathrm{x} \\ $$$$\Rightarrow\mathrm{x}\:=\:\mathrm{2}+\frac{\mathrm{3}}{\mathrm{x}}\:;\:\mathrm{x}^{\mathrm{2}} −\mathrm{2x}−\mathrm{3}=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{x}−\mathrm{3}\right)\left(\mathrm{x}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}\:=\:\mathrm{3}\:\mathrm{or}\:\mathrm{x}=−\mathrm{1}\left(\mathrm{rejected}\right) \\ $$$$\mathrm{then}\:\mathrm{5}\:+\frac{\mathrm{2}}{\mathrm{x}}\:=\:\mathrm{5}+\frac{\mathrm{2}}{\mathrm{3}}=\frac{\mathrm{17}}{\mathrm{3}}\: \\ $$

Answered by Ar Brandon last updated on 04/Aug/21

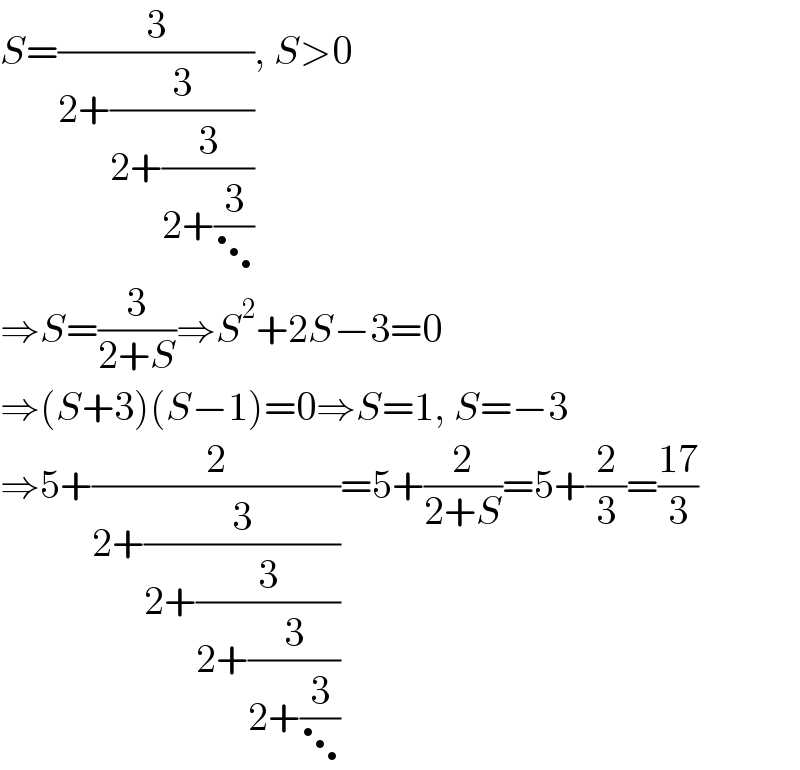
S=(3/(2+(3/(2+(3/(2+(3/⋱))))))), S>0 ⇒S=(3/(2+S))⇒S^2 +2S−3=0 ⇒(S+3)(S−1)=0⇒S=1, S=−3 ⇒5+(2/(2+(3/(2+(3/(2+(3/(2+(3/⋱)))))))))=5+(2/(2+S))=5+(2/3)=((17)/3)

$${S}=\frac{\mathrm{3}}{\mathrm{2}+\frac{\mathrm{3}}{\mathrm{2}+\frac{\mathrm{3}}{\mathrm{2}+\frac{\mathrm{3}}{\ddots}}}},\:{S}>\mathrm{0} \\ $$$$\Rightarrow{S}=\frac{\mathrm{3}}{\mathrm{2}+{S}}\Rightarrow{S}^{\mathrm{2}} +\mathrm{2}{S}−\mathrm{3}=\mathrm{0} \\ $$$$\Rightarrow\left({S}+\mathrm{3}\right)\left({S}−\mathrm{1}\right)=\mathrm{0}\Rightarrow{S}=\mathrm{1},\:{S}=−\mathrm{3} \\ $$$$\Rightarrow\mathrm{5}+\frac{\mathrm{2}}{\mathrm{2}+\frac{\mathrm{3}}{\mathrm{2}+\frac{\mathrm{3}}{\mathrm{2}+\frac{\mathrm{3}}{\mathrm{2}+\frac{\mathrm{3}}{\ddots}}}}}=\mathrm{5}+\frac{\mathrm{2}}{\mathrm{2}+{S}}=\mathrm{5}+\frac{\mathrm{2}}{\mathrm{3}}=\frac{\mathrm{17}}{\mathrm{3}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply