Question Number 149372 by fotosy2k last updated on 05/Aug/21

Answered by john_santu last updated on 05/Aug/21
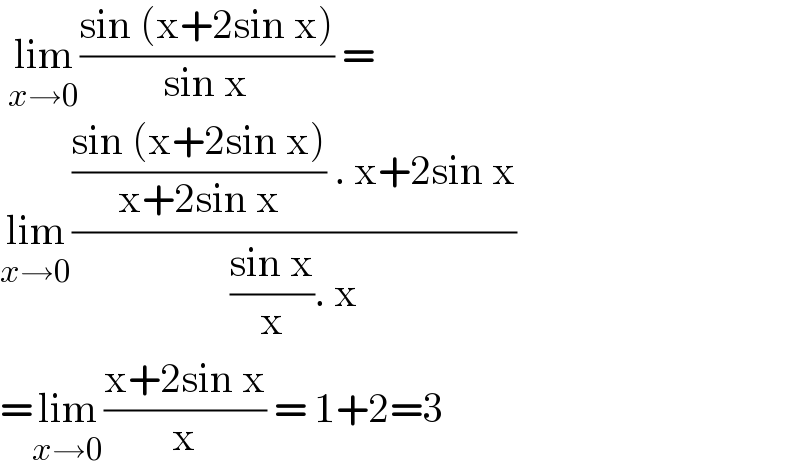
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\left(\mathrm{x}+\mathrm{2sin}\:\mathrm{x}\right)}{\mathrm{sin}\:\mathrm{x}}\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{sin}\:\left(\mathrm{x}+\mathrm{2sin}\:\mathrm{x}\right)}{\mathrm{x}+\mathrm{2sin}\:\mathrm{x}}\:.\:\mathrm{x}+\mathrm{2sin}\:\mathrm{x}}{\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{x}}.\:\mathrm{x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{x}+\mathrm{2sin}\:\mathrm{x}}{\mathrm{x}}\:=\:\mathrm{1}+\mathrm{2}=\mathrm{3} \\ $$
Commented by fotosy2k last updated on 05/Aug/21

$${thank}\:{you} \\ $$
