Question-149385

Question Number 149385 by liberty last updated on 05/Aug/21

Answered by Ar Brandon last updated on 05/Aug/21

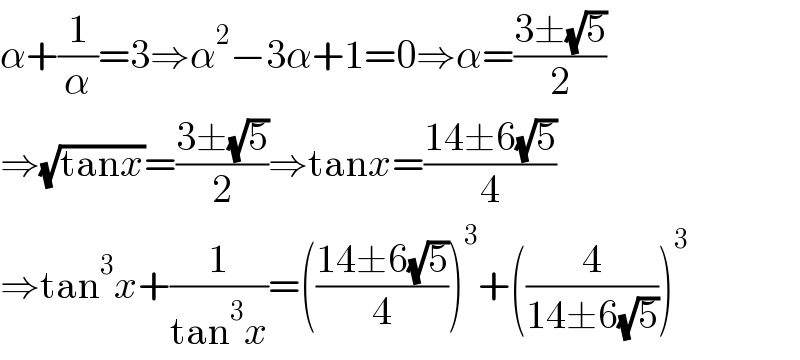
α+(1/α)=3⇒α^2 −3α+1=0⇒α=((3±(√5))/2) ⇒(√(tanx))=((3±(√5))/2)⇒tanx=((14±6(√5))/4) ⇒tan^3 x+(1/(tan^3 x))=(((14±6(√5))/4))^3 +((4/(14±6(√5))))^3

$$\alpha+\frac{\mathrm{1}}{\alpha}=\mathrm{3}\Rightarrow\alpha^{\mathrm{2}} −\mathrm{3}\alpha+\mathrm{1}=\mathrm{0}\Rightarrow\alpha=\frac{\mathrm{3}\pm\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\Rightarrow\sqrt{\mathrm{tan}{x}}=\frac{\mathrm{3}\pm\sqrt{\mathrm{5}}}{\mathrm{2}}\Rightarrow\mathrm{tan}{x}=\frac{\mathrm{14}\pm\mathrm{6}\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{tan}^{\mathrm{3}} {x}+\frac{\mathrm{1}}{\mathrm{tan}^{\mathrm{3}} {x}}=\left(\frac{\mathrm{14}\pm\mathrm{6}\sqrt{\mathrm{5}}}{\mathrm{4}}\right)^{\mathrm{3}} +\left(\frac{\mathrm{4}}{\mathrm{14}\pm\mathrm{6}\sqrt{\mathrm{5}}}\right)^{\mathrm{3}} \\ $$

Answered by Rasheed.Sindhi last updated on 05/Aug/21

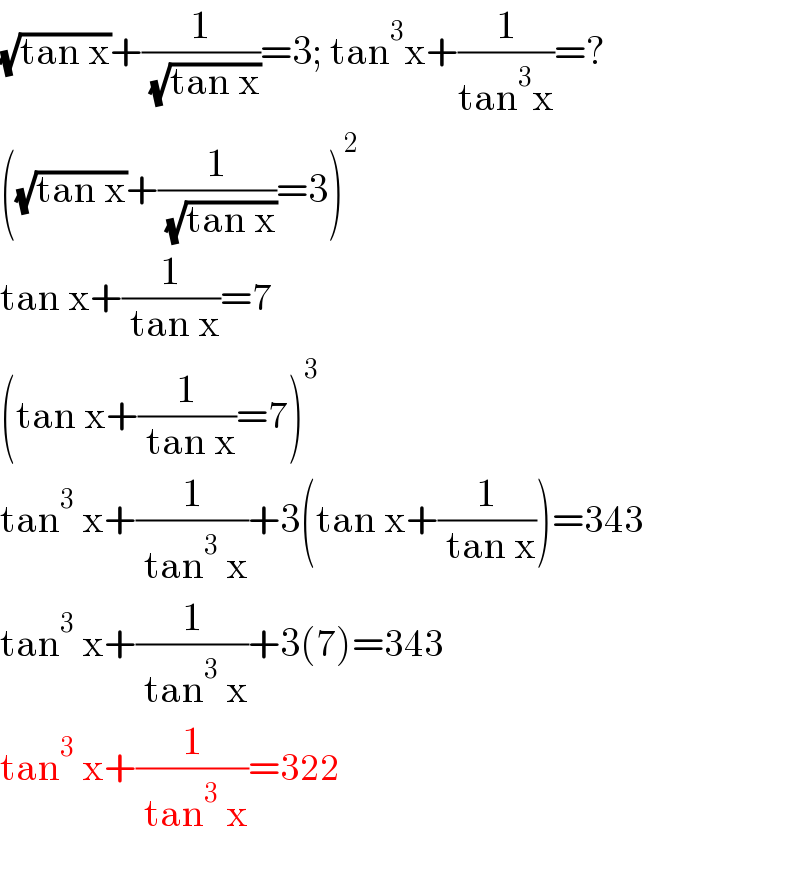
(√(tan x))+(1/( (√(tan x))))=3; tan^3 x+(1/(tan^3 x))=? ((√(tan x))+(1/( (√(tan x))))=3)^2 tan x+(1/( tan x))=7 (tan x+(1/( tan x))=7)^3 tan^3 x+(1/( tan^3 x))+3(tan x+(1/( tan x)))=343 tan^3 x+(1/( tan^3 x))+3(7)=343 tan^3 x+(1/( tan^3 x))=322

$$\sqrt{\mathrm{tan}\:\mathrm{x}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{tan}\:\mathrm{x}}}=\mathrm{3};\:\mathrm{tan}^{\mathrm{3}} \mathrm{x}+\frac{\mathrm{1}}{\mathrm{tan}^{\mathrm{3}} \mathrm{x}}=? \\ $$$$\left(\sqrt{\mathrm{tan}\:\mathrm{x}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{tan}\:\mathrm{x}}}=\mathrm{3}\right)^{\mathrm{2}} \\ $$$$\mathrm{tan}\:\mathrm{x}+\frac{\mathrm{1}}{\:\mathrm{tan}\:\mathrm{x}}=\mathrm{7} \\ $$$$\left(\mathrm{tan}\:\mathrm{x}+\frac{\mathrm{1}}{\:\mathrm{tan}\:\mathrm{x}}=\mathrm{7}\right)^{\mathrm{3}} \\ $$$$\mathrm{tan}^{\mathrm{3}} \:\mathrm{x}+\frac{\mathrm{1}}{\:\mathrm{tan}^{\mathrm{3}} \:\mathrm{x}}+\mathrm{3}\left(\mathrm{tan}\:\mathrm{x}+\frac{\mathrm{1}}{\:\mathrm{tan}\:\mathrm{x}}\right)=\mathrm{343} \\ $$$$\mathrm{tan}^{\mathrm{3}} \:\mathrm{x}+\frac{\mathrm{1}}{\:\mathrm{tan}^{\mathrm{3}} \:\mathrm{x}}+\mathrm{3}\left(\mathrm{7}\right)=\mathrm{343} \\ $$$$\mathrm{tan}^{\mathrm{3}} \:\mathrm{x}+\frac{\mathrm{1}}{\:\mathrm{tan}^{\mathrm{3}} \:\mathrm{x}}=\mathrm{322} \\ $$$$ \\ $$

Answered by liberty last updated on 05/Aug/21

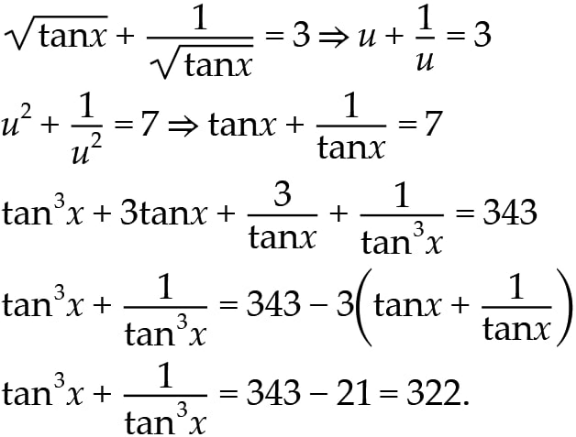
Answered by Rasheed.Sindhi last updated on 05/Aug/21

(√(tan x))+(1/( (√(tan x))))=3; tan^3 x+(1/(tan^3 x))=? ((√(tan x))+(1/( (√(tan x))))=3)^3 tan^(3/2) x+(1/(tan^(3/2) x))+3((√(tan x))+(1/( (√(tan x)))))=27 tan^(3/2) x+(1/(tan^(3/2) x))+3(3)=27 tan^(3/2) x+(1/(tan^(3/2) x))+3(3)=27 tan^(3/2) x+(1/(tan^(3/2) x))=18 (tan^(3/2) +(1/(tan^(3/2) ))=18)^2 tan^3 x+(1/(tan^3 x))=324−2=322

$$\sqrt{\mathrm{tan}\:\mathrm{x}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{tan}\:\mathrm{x}}}=\mathrm{3};\:\mathrm{tan}^{\mathrm{3}} \mathrm{x}+\frac{\mathrm{1}}{\mathrm{tan}^{\mathrm{3}} \mathrm{x}}=? \\ $$$$\left(\sqrt{\mathrm{tan}\:\mathrm{x}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{tan}\:\mathrm{x}}}=\mathrm{3}\right)^{\mathrm{3}} \\ $$$$\mathrm{tan}^{\mathrm{3}/\mathrm{2}} \mathrm{x}+\frac{\mathrm{1}}{\mathrm{tan}^{\mathrm{3}/\mathrm{2}} \mathrm{x}}+\mathrm{3}\left(\sqrt{\mathrm{tan}\:\mathrm{x}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{tan}\:\mathrm{x}}}\right)=\mathrm{27} \\ $$$$\mathrm{tan}^{\mathrm{3}/\mathrm{2}} \mathrm{x}+\frac{\mathrm{1}}{\mathrm{tan}^{\mathrm{3}/\mathrm{2}} \mathrm{x}}+\mathrm{3}\left(\mathrm{3}\right)=\mathrm{27} \\ $$$$\mathrm{tan}^{\mathrm{3}/\mathrm{2}} \mathrm{x}+\frac{\mathrm{1}}{\mathrm{tan}^{\mathrm{3}/\mathrm{2}} \mathrm{x}}+\mathrm{3}\left(\mathrm{3}\right)=\mathrm{27} \\ $$$$\mathrm{tan}^{\mathrm{3}/\mathrm{2}} \mathrm{x}+\frac{\mathrm{1}}{\mathrm{tan}^{\mathrm{3}/\mathrm{2}} \mathrm{x}}=\mathrm{18} \\ $$$$\left(\mathrm{tan}^{\mathrm{3}/\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{tan}^{\mathrm{3}/\mathrm{2}} }=\mathrm{18}\right)^{\mathrm{2}} \\ $$$$\mathrm{tan}^{\mathrm{3}} \mathrm{x}+\frac{\mathrm{1}}{\mathrm{tan}^{\mathrm{3}} \mathrm{x}}=\mathrm{324}−\mathrm{2}=\mathrm{322} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply