Question Number 149395 by mathdanisur last updated on 05/Aug/21

Answered by Olaf_Thorendsen last updated on 05/Aug/21
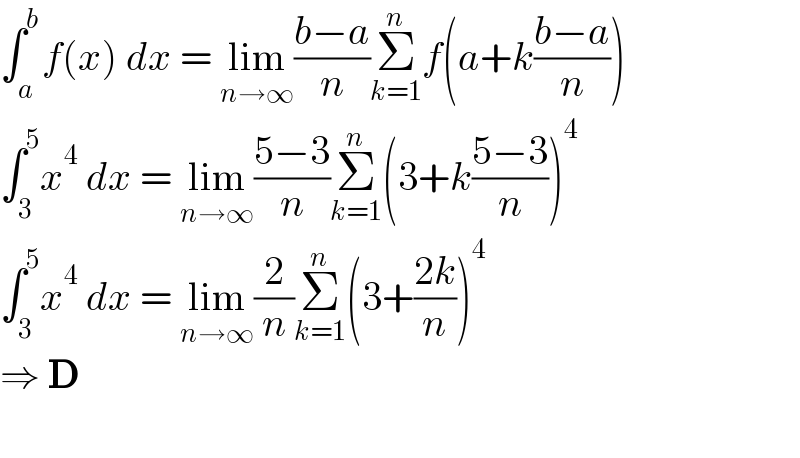
$$\int_{{a}} ^{{b}} {f}\left({x}\right)\:{dx}\:=\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{b}−{a}}{{n}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{f}\left({a}+{k}\frac{{b}−{a}}{{n}}\right) \\ $$$$\int_{\mathrm{3}} ^{\mathrm{5}} {x}^{\mathrm{4}} \:{dx}\:=\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{5}−\mathrm{3}}{{n}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\mathrm{3}+{k}\frac{\mathrm{5}−\mathrm{3}}{{n}}\right)^{\mathrm{4}} \\ $$$$\int_{\mathrm{3}} ^{\mathrm{5}} {x}^{\mathrm{4}} \:{dx}\:=\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{2}}{{n}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\mathrm{3}+\frac{\mathrm{2}{k}}{{n}}\right)^{\mathrm{4}} \\ $$$$\Rightarrow\:\boldsymbol{\mathrm{D}} \\ $$$$ \\ $$
Commented by mathdanisur last updated on 05/Aug/21

$${Ser},\:{Thank}\:{You} \\ $$
