Question-149400

Question Number 149400 by mathdanisur last updated on 05/Aug/21

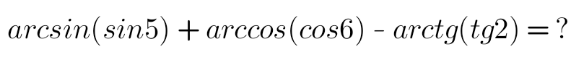
Answered by liberty last updated on 05/Aug/21

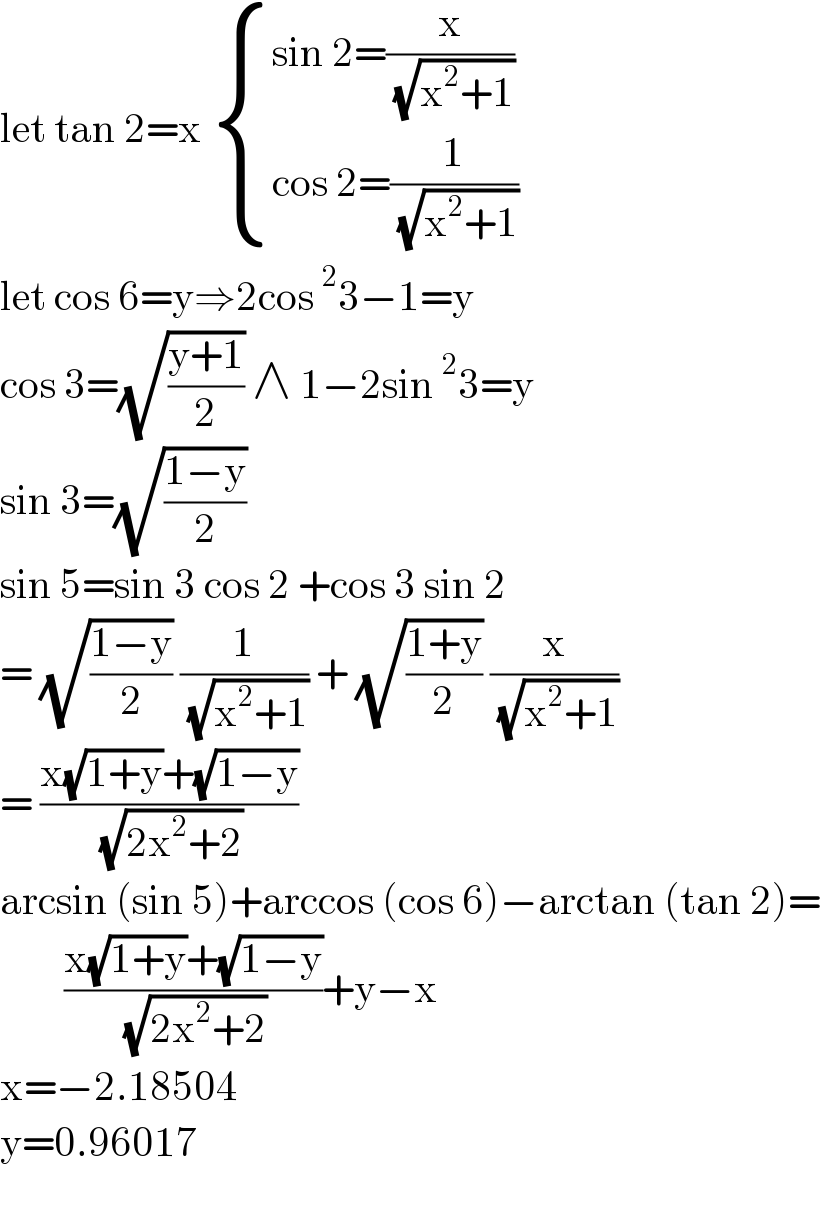
let tan 2=x { ((sin 2=(x/( (√(x^2 +1)))))),((cos 2=(1/( (√(x^2 +1)))))) :} let cos 6=y⇒2cos^2 3−1=y cos 3=(√((y+1)/2)) ∧ 1−2sin^2 3=y sin 3=(√((1−y)/2)) sin 5=sin 3 cos 2 +cos 3 sin 2 = (√((1−y)/2)) (1/( (√(x^2 +1)))) + (√((1+y)/2)) (x/( (√(x^2 +1)))) = ((x(√(1+y))+(√(1−y)))/( (√(2x^2 +2)))) arcsin (sin 5)+arccos (cos 6)−arctan (tan 2)= ((x(√(1+y))+(√(1−y)))/( (√(2x^2 +2))))+y−x x=−2.18504 y=0.96017

$$\mathrm{let}\:\mathrm{tan}\:\mathrm{2}=\mathrm{x}\:\begin{cases}{\mathrm{sin}\:\mathrm{2}=\frac{\mathrm{x}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}}}\\{\mathrm{cos}\:\mathrm{2}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}}}\end{cases} \\ $$$$\mathrm{let}\:\mathrm{cos}\:\mathrm{6}=\mathrm{y}\Rightarrow\mathrm{2cos}\:^{\mathrm{2}} \mathrm{3}−\mathrm{1}=\mathrm{y} \\ $$$$\mathrm{cos}\:\mathrm{3}=\sqrt{\frac{\mathrm{y}+\mathrm{1}}{\mathrm{2}}}\:\wedge\:\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \mathrm{3}=\mathrm{y} \\ $$$$\mathrm{sin}\:\mathrm{3}=\sqrt{\frac{\mathrm{1}−\mathrm{y}}{\mathrm{2}}} \\ $$$$\mathrm{sin}\:\mathrm{5}=\mathrm{sin}\:\mathrm{3}\:\mathrm{cos}\:\mathrm{2}\:+\mathrm{cos}\:\mathrm{3}\:\mathrm{sin}\:\mathrm{2} \\ $$$$=\:\sqrt{\frac{\mathrm{1}−\mathrm{y}}{\mathrm{2}}}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}}\:+\:\sqrt{\frac{\mathrm{1}+\mathrm{y}}{\mathrm{2}}}\:\frac{\mathrm{x}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}} \\ $$$$=\:\frac{\mathrm{x}\sqrt{\mathrm{1}+\mathrm{y}}+\sqrt{\mathrm{1}−\mathrm{y}}}{\:\sqrt{\mathrm{2x}^{\mathrm{2}} +\mathrm{2}}} \\ $$$$\mathrm{arcsin}\:\left(\mathrm{sin}\:\mathrm{5}\right)+\mathrm{arccos}\:\left(\mathrm{cos}\:\mathrm{6}\right)−\mathrm{arctan}\:\left(\mathrm{tan}\:\mathrm{2}\right)= \\ $$$$\:\:\:\:\:\:\:\:\frac{\mathrm{x}\sqrt{\mathrm{1}+\mathrm{y}}+\sqrt{\mathrm{1}−\mathrm{y}}}{\:\sqrt{\mathrm{2x}^{\mathrm{2}} +\mathrm{2}}}+\mathrm{y}−\mathrm{x} \\ $$$$\mathrm{x}=−\mathrm{2}.\mathrm{18504} \\ $$$$\mathrm{y}=\mathrm{0}.\mathrm{96017} \\ $$$$ \\ $$

Commented by mathdanisur last updated on 05/Aug/21

$${Thank}\:{You}\:{Ser} \\ $$

Answered by dumitrel last updated on 05/Aug/21

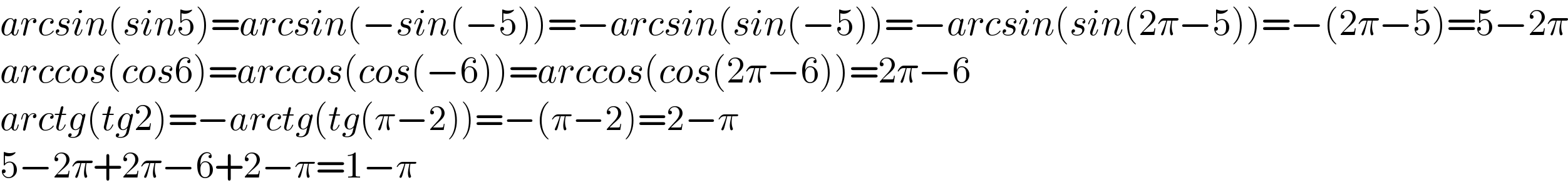
arcsin(sin5)=arcsin(−sin(−5))=−arcsin(sin(−5))=−arcsin(sin(2π−5))=−(2π−5)=5−2π arccos(cos6)=arccos(cos(−6))=arccos(cos(2π−6))=2π−6 arctg(tg2)=−arctg(tg(π−2))=−(π−2)=2−π 5−2π+2π−6+2−π=1−π

$${arcsin}\left({sin}\mathrm{5}\right)={arcsin}\left(−{sin}\left(−\mathrm{5}\right)\right)=−{arcsin}\left({sin}\left(−\mathrm{5}\right)\right)=−{arcsin}\left({sin}\left(\mathrm{2}\pi−\mathrm{5}\right)\right)=−\left(\mathrm{2}\pi−\mathrm{5}\right)=\mathrm{5}−\mathrm{2}\pi \\ $$$${arccos}\left({cos}\mathrm{6}\right)={arccos}\left({cos}\left(−\mathrm{6}\right)\right)={arccos}\left({cos}\left(\mathrm{2}\pi−\mathrm{6}\right)\right)=\mathrm{2}\pi−\mathrm{6} \\ $$$${arctg}\left({tg}\mathrm{2}\right)=−{arctg}\left({tg}\left(\pi−\mathrm{2}\right)\right)=−\left(\pi−\mathrm{2}\right)=\mathrm{2}−\pi \\ $$$$\mathrm{5}−\mathrm{2}\pi+\mathrm{2}\pi−\mathrm{6}+\mathrm{2}−\pi=\mathrm{1}−\pi \\ $$

Commented by mathdanisur last updated on 05/Aug/21

$${Ser},\:{Thank}\:{You} \\ $$

Commented by liberty last updated on 05/Aug/21

$$\mathrm{false} \\ $$

Commented by liberty last updated on 05/Aug/21

Answered by MJS_new last updated on 05/Aug/21

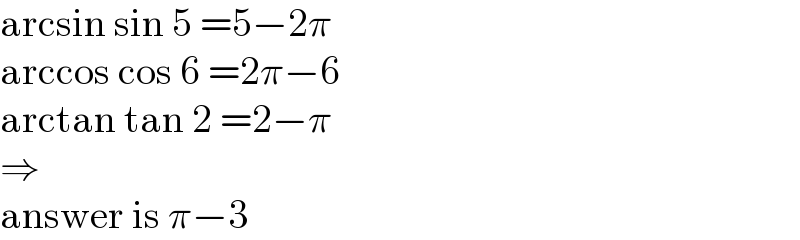
arcsin sin 5 =5−2π arccos cos 6 =2π−6 arctan tan 2 =2−π ⇒ answer is π−3

$$\mathrm{arcsin}\:\mathrm{sin}\:\mathrm{5}\:=\mathrm{5}−\mathrm{2}\pi \\ $$$$\mathrm{arccos}\:\mathrm{cos}\:\mathrm{6}\:=\mathrm{2}\pi−\mathrm{6} \\ $$$$\mathrm{arctan}\:\mathrm{tan}\:\mathrm{2}\:=\mathrm{2}−\pi \\ $$$$\Rightarrow \\ $$$$\mathrm{answer}\:\mathrm{is}\:\pi−\mathrm{3} \\ $$

Commented by mathdanisur last updated on 06/Aug/21

$$\mathrm{Thankyou}\:\boldsymbol{\mathrm{Ser}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply