Question Number 149425 by help last updated on 05/Aug/21

Answered by dumitrel last updated on 05/Aug/21
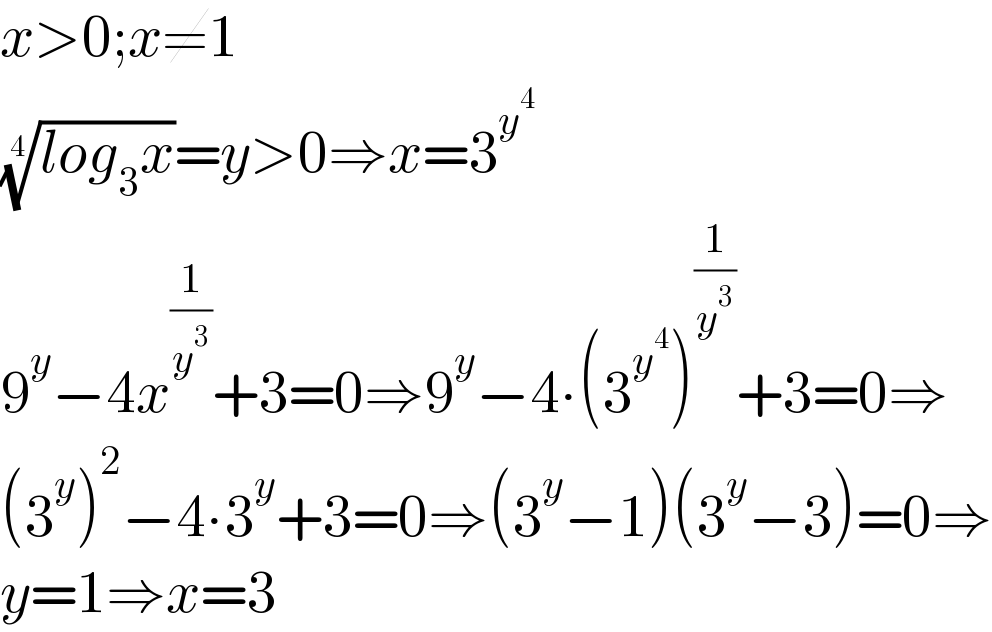
$${x}>\mathrm{0};{x}\neq\mathrm{1} \\ $$$$\sqrt[{\mathrm{4}}]{{log}_{\mathrm{3}} {x}}={y}>\mathrm{0}\Rightarrow{x}=\mathrm{3}^{{y}^{\mathrm{4}} } \\ $$$$\mathrm{9}^{{y}} −\mathrm{4}{x}^{\frac{\mathrm{1}}{{y}^{\mathrm{3}} }} +\mathrm{3}=\mathrm{0}\Rightarrow\mathrm{9}^{{y}} −\mathrm{4}\centerdot\left(\mathrm{3}^{{y}^{\mathrm{4}} } \right)^{\frac{\mathrm{1}}{{y}^{\mathrm{3}} }} +\mathrm{3}=\mathrm{0}\Rightarrow \\ $$$$\left(\mathrm{3}^{{y}} \right)^{\mathrm{2}} −\mathrm{4}\centerdot\mathrm{3}^{{y}} +\mathrm{3}=\mathrm{0}\Rightarrow\left(\mathrm{3}^{{y}} −\mathrm{1}\right)\left(\mathrm{3}^{{y}} −\mathrm{3}\right)=\mathrm{0}\Rightarrow \\ $$$${y}=\mathrm{1}\Rightarrow{x}=\mathrm{3} \\ $$
