Question Number 149457 by liberty last updated on 05/Aug/21
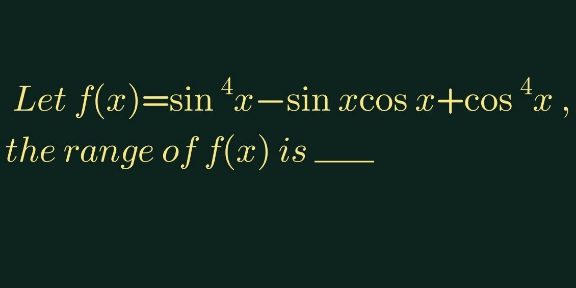
Answered by EDWIN88 last updated on 05/Aug/21

$$\:{f}\left({x}\right)=\mathrm{sin}\:^{\mathrm{4}} {x}−\mathrm{sin}\:{x}\mathrm{cos}\:{x}+\mathrm{cos}\:^{\mathrm{4}} {x} \\ $$$${f}\left({x}\right)=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{2}{x}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:^{\mathrm{2}} \mathrm{2}{x} \\ $$$${we}\:{define}\:\mathrm{sin}\:\mathrm{2}{x}={t} \\ $$$${f}\left({x}\right)={g}\left({t}\right)=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{t}−\frac{\mathrm{1}}{\mathrm{2}}{t}^{\mathrm{2}} \\ $$$${g}\left({t}\right)=\frac{\mathrm{9}}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{2}}\left({t}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$${so}\:{we}\:{have}\:\underset{−\mathrm{1}\leqslant{t}\leqslant\mathrm{1}} {\underbrace{{min}}}\:{g}\left({t}\right)={g}\left(\mathrm{1}\right)=\mathrm{0} \\ $$$${and}\:\underset{−\mathrm{1}\leqslant{t}\leqslant\mathrm{1}} {\underbrace{{max}}}\:{g}\left({t}\right)={g}\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\mathrm{9}}{\mathrm{8}} \\ $$$${Hence}\:\mathrm{0}\leqslant{f}\left({x}\right)\leqslant\frac{\mathrm{9}}{\mathrm{8}} \\ $$
