Question Number 149458 by mathdanisur last updated on 05/Aug/21

Commented by EDWIN88 last updated on 06/Aug/21

$${n}\left({S}\right)={C}_{\mathrm{2}} ^{\mathrm{7}} =\frac{\mathrm{7}×\mathrm{6}}{\mathrm{2}×\mathrm{1}}=\mathrm{21} \\ $$$${n}\left({A}\right)=\:\mathrm{18} \\ $$$${A}=\left\{\left(\mathrm{1},\mathrm{2}\right),\left(\mathrm{1},\mathrm{4}\right),\left(\mathrm{1},\mathrm{6}\right),\left(\mathrm{2},\mathrm{3}\right),\left(\mathrm{2},\mathrm{4}\right),\right. \\ $$$$\:\:\:\:\:\left(\mathrm{2},\mathrm{5}\right),\left(\mathrm{2},\mathrm{6}\right),\left(\mathrm{3},\mathrm{4}\right),\left(\mathrm{3},\mathrm{6}\right),\left(\mathrm{4},\mathrm{5}\right),\left(\mathrm{4},\mathrm{6}\right), \\ $$$$\:\:\:\:\left(\mathrm{5},\mathrm{6}\right),\left(\mathrm{0},\mathrm{1}\right),\left(\mathrm{0},\mathrm{2}\right),\left(\mathrm{0},\mathrm{3}\right),\left(\mathrm{0},\mathrm{4}\right),\left(\mathrm{0},\mathrm{5}\right) \\ $$$$\left.\:\:,\left(\mathrm{0},\mathrm{6}\right)\right\} \\ $$$${then}\:{P}\left({A}\right)=\frac{\mathrm{18}}{\mathrm{21}}\:=\frac{\mathrm{6}}{\mathrm{7}} \\ $$
Commented by EDWIN88 last updated on 06/Aug/21
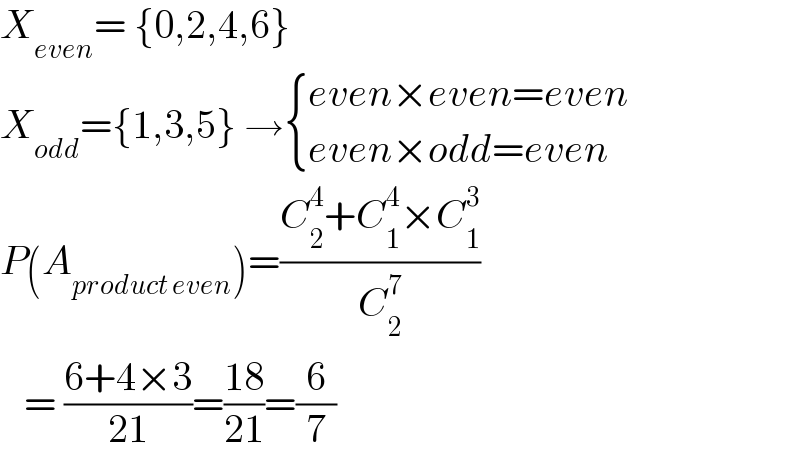
$${X}_{{even}} =\:\left\{\mathrm{0},\mathrm{2},\mathrm{4},\mathrm{6}\right\} \\ $$$${X}_{{odd}} =\left\{\mathrm{1},\mathrm{3},\mathrm{5}\right\}\:\rightarrow\begin{cases}{{even}×{even}={even}}\\{{even}×{odd}={even}}\end{cases} \\ $$$${P}\left({A}_{{product}\:{even}} \right)=\frac{{C}_{\mathrm{2}} ^{\mathrm{4}} +{C}_{\mathrm{1}} ^{\mathrm{4}} ×{C}_{\mathrm{1}} ^{\mathrm{3}} }{{C}_{\mathrm{2}} ^{\mathrm{7}} } \\ $$$$\:\:\:=\:\frac{\mathrm{6}+\mathrm{4}×\mathrm{3}}{\mathrm{21}}=\frac{\mathrm{18}}{\mathrm{21}}=\frac{\mathrm{6}}{\mathrm{7}} \\ $$
Commented by mathdanisur last updated on 06/Aug/21

$$\mathrm{Thanlyou}\:\boldsymbol{\mathrm{Ser}} \\ $$
Answered by mr W last updated on 05/Aug/21

$${p}=\mathrm{1}−\frac{\mathrm{6}+{C}_{\mathrm{2}} ^{\mathrm{3}} }{{C}_{\mathrm{2}} ^{\mathrm{7}} }=\mathrm{1}−\frac{\mathrm{9}}{\mathrm{21}}=\frac{\mathrm{4}}{\mathrm{7}} \\ $$
Commented by mathdanisur last updated on 05/Aug/21

$$\mathrm{Thank}\:\mathrm{you}\:\boldsymbol{\mathrm{Ser}},\:\mathrm{but}\:\mathrm{answer}:\:\:\frac{\mathrm{2}}{\mathrm{15}} \\ $$
Commented by mr W last updated on 05/Aug/21
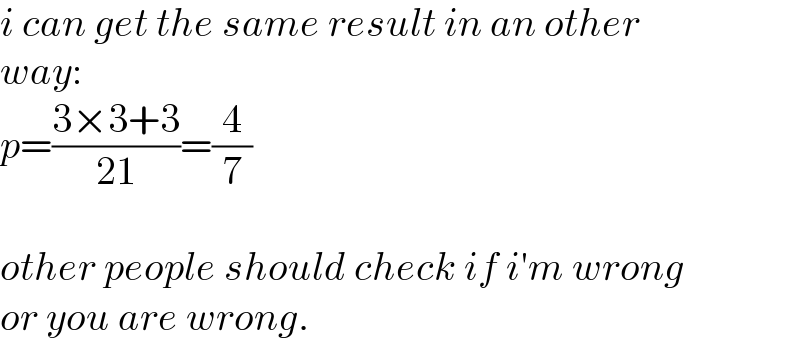
$${i}\:{can}\:{get}\:{the}\:{same}\:{result}\:{in}\:{an}\:{other} \\ $$$${way}: \\ $$$${p}=\frac{\mathrm{3}×\mathrm{3}+\mathrm{3}}{\mathrm{21}}=\frac{\mathrm{4}}{\mathrm{7}} \\ $$$$ \\ $$$${other}\:{people}\:{should}\:{check}\:{if}\:{i}'{m}\:{wrong} \\ $$$${or}\:{you}\:{are}\:{wrong}. \\ $$
Commented by mathdanisur last updated on 05/Aug/21

$$\mathrm{Thankyou}\:\boldsymbol{\mathrm{S}}\mathrm{er} \\ $$
Commented by EDWIN88 last updated on 06/Aug/21
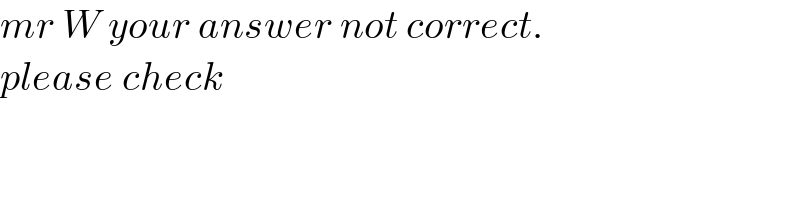
$${mr}\:{W}\:{your}\:{answer}\:{not}\:{correct}. \\ $$$${please}\:{check} \\ $$
Commented by mr W last updated on 06/Aug/21

$${i}\:{excluded}\:{zero}. \\ $$$${p}=\mathrm{1}−\frac{\mathrm{6}+{C}_{\mathrm{2}} ^{\mathrm{3}} }{{C}_{\mathrm{2}} ^{\mathrm{7}} }=\mathrm{1}−\frac{\mathrm{9}}{\mathrm{21}}=\frac{\mathrm{4}}{\mathrm{7}} \\ $$$${if}\:{zero}\:{is}\:{included},\:{then} \\ $$$${p}=\mathrm{1}−\frac{{C}_{\mathrm{2}} ^{\mathrm{3}} }{{C}_{\mathrm{2}} ^{\mathrm{7}} }=\mathrm{1}−\frac{\mathrm{3}}{\mathrm{21}}=\frac{\mathrm{6}}{\mathrm{7}} \\ $$
Commented by mathdanisur last updated on 06/Aug/21

$$\mathrm{Thankyou}\:\boldsymbol{\mathrm{Ser}} \\ $$
