Question Number 149467 by fotosy2k last updated on 05/Aug/21
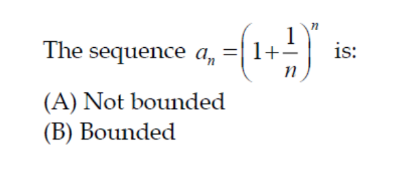
Answered by mindispower last updated on 05/Aug/21
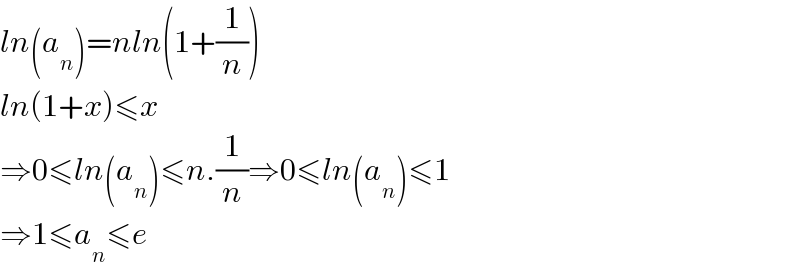
$${ln}\left({a}_{{n}} \right)={nln}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right) \\ $$$${ln}\left(\mathrm{1}+{x}\right)\leqslant{x} \\ $$$$\Rightarrow\mathrm{0}\leqslant{ln}\left({a}_{{n}} \right)\leqslant{n}.\frac{\mathrm{1}}{{n}}\Rightarrow\mathrm{0}\leqslant{ln}\left({a}_{{n}} \right)\leqslant\mathrm{1} \\ $$$$\Rightarrow\mathrm{1}\leqslant{a}_{{n}} \leqslant{e} \\ $$
