Question Number 149481 by mathdanisur last updated on 05/Aug/21

Answered by mr W last updated on 05/Aug/21

$${say}\:{AB}={CK}={x},\:{BM}={BK}=\mathrm{1} \\ $$$${AC}={x}−\mathrm{1}+{x}=\mathrm{2}{x}−\mathrm{1} \\ $$$$\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{2}} ={x}^{\mathrm{2}} +\left({x}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} =\mathrm{3}{x} \\ $$$$\Rightarrow{x}=\mathrm{3} \\ $$$$\Rightarrow{AB}=\mathrm{3},{BC}=\mathrm{4},{CA}=\mathrm{5} \\ $$$${AK}=\sqrt{\mathrm{3}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} }=\sqrt{\mathrm{10}} \\ $$$${AK}×{AH}={AM}^{\mathrm{2}} \\ $$$$\sqrt{\mathrm{10}}×{AH}=\mathrm{2}^{\mathrm{2}} \\ $$$${AH}=\frac{\mathrm{2}\sqrt{\mathrm{10}}}{\mathrm{5}} \\ $$$$\Rightarrow{HK}=\sqrt{\mathrm{10}}−\frac{\mathrm{2}\sqrt{\mathrm{10}}}{\mathrm{5}}=\frac{\mathrm{3}\sqrt{\mathrm{10}}}{\mathrm{5}} \\ $$$${HC}^{\mathrm{2}} =\mathrm{3}^{\mathrm{2}} +\left(\frac{\mathrm{3}\sqrt{\mathrm{10}}}{\mathrm{5}}\right)^{\mathrm{2}} +\mathrm{2}×\mathrm{3}×\frac{\mathrm{3}\sqrt{\mathrm{10}}}{\mathrm{5}}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{10}}} \\ $$$${HC}^{\mathrm{2}} =\frac{\mathrm{81}}{\mathrm{5}} \\ $$$${HC}=\frac{\mathrm{9}}{\:\sqrt{\mathrm{5}}} \\ $$$$\frac{\mathrm{sin}\:\theta}{\mathrm{3}}=\frac{\mathrm{3}}{\:\sqrt{\mathrm{10}}}×\frac{\sqrt{\mathrm{5}}}{\mathrm{9}} \\ $$$$\mathrm{sin}\:\theta=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow\theta=\mathrm{45}° \\ $$
Commented by mathdanisur last updated on 05/Aug/21

$$\mathrm{Thankyou}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{cool} \\ $$
Commented by Tawa11 last updated on 05/Aug/21

$$\mathrm{great}\:\mathrm{sir} \\ $$
Commented by Tawa11 last updated on 06/Aug/21

$$\mathrm{Sir}\:\:\mathrm{mrW}\:\:\:\mathrm{please}\:\mathrm{check}\:\mathrm{Q149510}.\:\mathrm{Geometry}.\:\:\mathrm{Your}\:\mathrm{approach}\:\mathrm{too}\:\mathrm{is}\:\mathrm{needed}. \\ $$$$\mathrm{Thanks}\:\mathrm{sir}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}. \\ $$
Commented by mr W last updated on 06/Aug/21
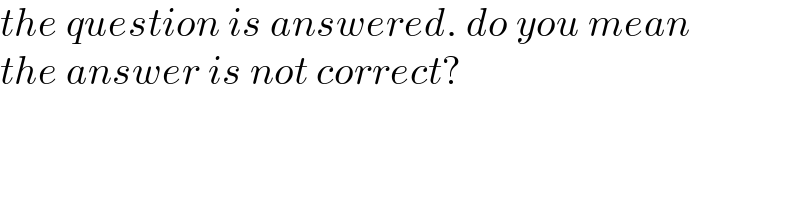
$${the}\:{question}\:{is}\:{answered}.\:{do}\:{you}\:{mean} \\ $$$${the}\:{answer}\:{is}\:{not}\:{correct}? \\ $$
Commented by Tawa11 last updated on 06/Aug/21

$$\mathrm{No}\:\mathrm{sir}.\:\mathrm{Just}\:\mathrm{to}\:\mathrm{see}\:\mathrm{another}\:\mathrm{approach}. \\ $$
Commented by Brahan last updated on 06/Aug/21

$$\boldsymbol{{why}}\:\boldsymbol{{BK}}=\boldsymbol{{BM}}=\mathrm{1} \\ $$
Commented by mr W last updated on 07/Aug/21
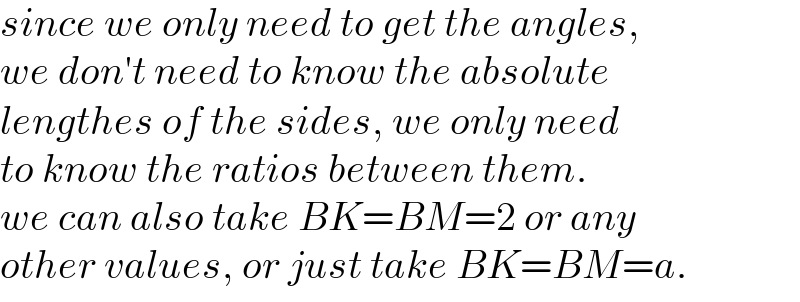
$${since}\:{we}\:{only}\:{need}\:{to}\:{get}\:{the}\:{angles}, \\ $$$${we}\:{don}'{t}\:{need}\:{to}\:{know}\:{the}\:{absolute} \\ $$$${lengthes}\:{of}\:{the}\:{sides},\:{we}\:{only}\:{need} \\ $$$${to}\:{know}\:{the}\:{ratios}\:{between}\:{them}. \\ $$$${we}\:{can}\:{also}\:{take}\:{BK}={BM}=\mathrm{2}\:{or}\:{any} \\ $$$${other}\:{values},\:{or}\:{just}\:{take}\:{BK}={BM}={a}. \\ $$
