Question Number 149527 by fotosy2k last updated on 06/Aug/21

Commented by fotosy2k last updated on 06/Aug/21

$${help}\:{me}\:{out} \\ $$$$ \\ $$
Answered by puissant last updated on 06/Aug/21
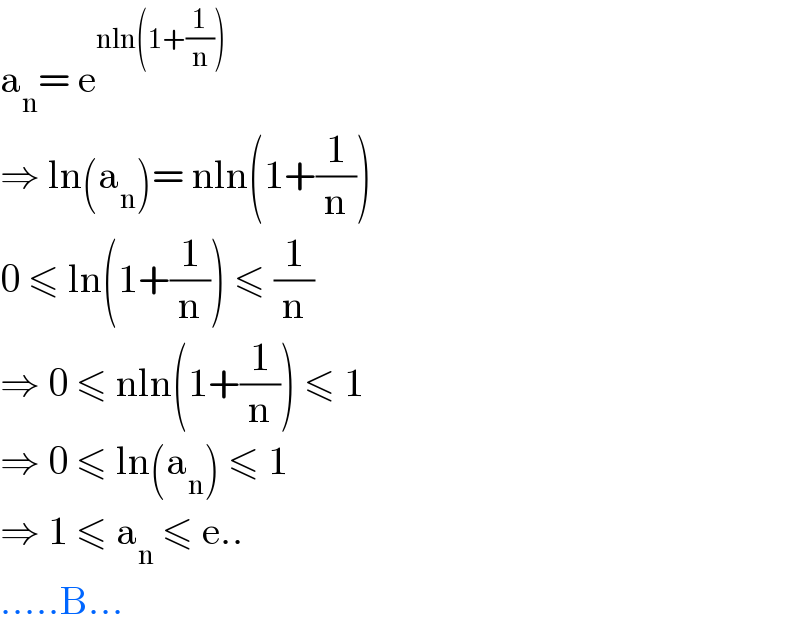
$$\mathrm{a}_{\mathrm{n}} =\:\mathrm{e}^{\mathrm{nln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}}\right)} \\ $$$$\Rightarrow\:\mathrm{ln}\left(\mathrm{a}_{\mathrm{n}} \right)=\:\mathrm{nln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}}\right) \\ $$$$\mathrm{0}\:\leqslant\:\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}}\right)\:\leqslant\:\frac{\mathrm{1}}{\mathrm{n}} \\ $$$$\Rightarrow\:\mathrm{0}\:\leqslant\:\mathrm{nln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}}\right)\:\leqslant\:\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{0}\:\leqslant\:\mathrm{ln}\left(\mathrm{a}_{\mathrm{n}} \right)\:\leqslant\:\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{1}\:\leqslant\:\mathrm{a}_{\mathrm{n}} \:\leqslant\:\mathrm{e}.. \\ $$$$…..\mathrm{B}… \\ $$
Commented by fotosy2k last updated on 06/Aug/21

$${thank}\:{u} \\ $$
