Menu Close

Question-149534

Tinku Tara 0 Comments
Pin




Question Number 149534 by ArielVyny last updated on 06/Aug/21
Answered by Olaf_Thorendsen last updated on 06/Aug/21
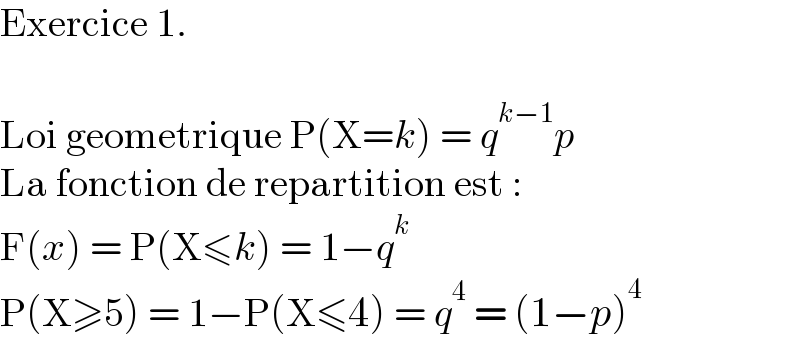
Exercice 1. Loi geometrique P(X=k) = q^(k−1) p La fonction de repartition est : F(x) = P(X≤k) = 1−q^k P(X≥5) = 1−P(X≤4) = q^4 = (1−p)^4
Exercice1.LoigeometriqueP(X=k)=qk−1pLafonctionderepartitionest:F(x)=P(X⩽k)=1−qkP(X⩾5)=1−P(X⩽4)=q4=(1−p)4
Answered by Olaf_Thorendsen last updated on 06/Aug/21
Exercice 2. 3 boules noires et 5 boules blanches. L′evenement A_3 est “premiere boule noire au 3eme tirage”. Pour realiser A_3 , il faut realiser 3 evenements successifs : −une boule blanche au 1er tirage avec une probabilite (5/8). −une boule blanche au 2eme tirage avec une probabilite (4/7). −une boule noire au 3eme tirage avec une probabilite (3/6) = (1/2). P(A_3 ) = (5/8)×(4/7)×(1/2) = (5/(28)) ≈ 17,9%.
Exercice2.3boulesnoireset5boulesblanches.L′evenementA3est“premiereboulenoireau3emetirage″.PourrealiserA3,ilfautrealiser3evenementssuccessifs:−unebouleblancheau1ertirageavecuneprobabilite58.−unebouleblancheau2emetirageavecuneprobabilite47.−uneboulenoireau3emetirageavecuneprobabilite36=12.P(A3)=58×47×12=528≈17,9%.

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *