Question Number 149636 by SLVR last updated on 06/Aug/21

Answered by mr W last updated on 06/Aug/21
![Q1 x is integer, then x^2 also integer. [x^2 ]=x^2 =x+1 which has no solution. ⇒answer C)](https://www.tinkutara.com/question/Q149641.png)
$${Q}\mathrm{1} \\ $$$${x}\:{is}\:{integer},\:{then}\:{x}^{\mathrm{2}} \:{also}\:{integer}. \\ $$$$\left[{x}^{\mathrm{2}} \right]={x}^{\mathrm{2}} ={x}+\mathrm{1}\:{which}\:{has}\:{no}\:{solution}. \\ $$$$\left.\Rightarrow{answer}\:{C}\right) \\ $$
Commented by SLVR last updated on 06/Aug/21
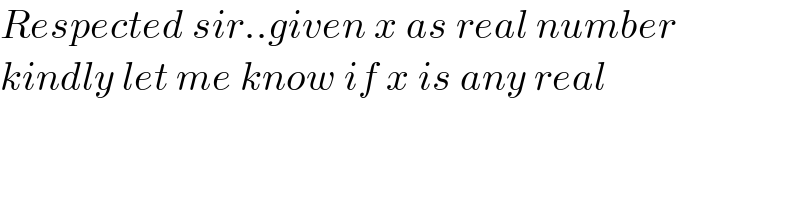
$${Respected}\:{sir}..{given}\:{x}\:{as}\:{real}\:{number} \\ $$$${kindly}\:{let}\:{me}\:{know}\:{if}\:{x}\:{is}\:{any}\:{real} \\ $$
Commented by mr W last updated on 06/Aug/21
![[x^2 ] is integer, and x=[x^2 ]−1, so x is also integer. when x is integer, then x^2 is also integer. when x^2 is integer, then [x^2 ]=x^2 . when [x^2 ]=x^2 , then the equation becomes x^2 =x+1 with x∈Z. and it has no solution.](https://www.tinkutara.com/question/Q149652.png)
$$\left[{x}^{\mathrm{2}} \right]\:{is}\:{integer},\:{and}\:{x}=\left[{x}^{\mathrm{2}} \right]−\mathrm{1},\:{so}\:{x} \\ $$$${is}\:{also}\:{integer}.\:{when}\:{x}\:{is}\:{integer}, \\ $$$${then}\:{x}^{\mathrm{2}} \:{is}\:{also}\:{integer}.\:{when}\:{x}^{\mathrm{2}} \:{is} \\ $$$${integer},\:{then}\:\left[{x}^{\mathrm{2}} \right]={x}^{\mathrm{2}} .\:{when}\:\left[{x}^{\mathrm{2}} \right]={x}^{\mathrm{2}} , \\ $$$${then}\:{the}\:{equation}\:{becomes} \\ $$$${x}^{\mathrm{2}} ={x}+\mathrm{1}\:{with}\:{x}\in{Z}.\:{and}\:{it}\:{has}\:{no} \\ $$$${solution}. \\ $$
Commented by SLVR last updated on 06/Aug/21
$${great}….{understood}..{Thanks}\:{Prof}.{W} \\ $$
