Question Number 149637 by mnjuly1970 last updated on 06/Aug/21

Answered by iloveisrael last updated on 06/Aug/21
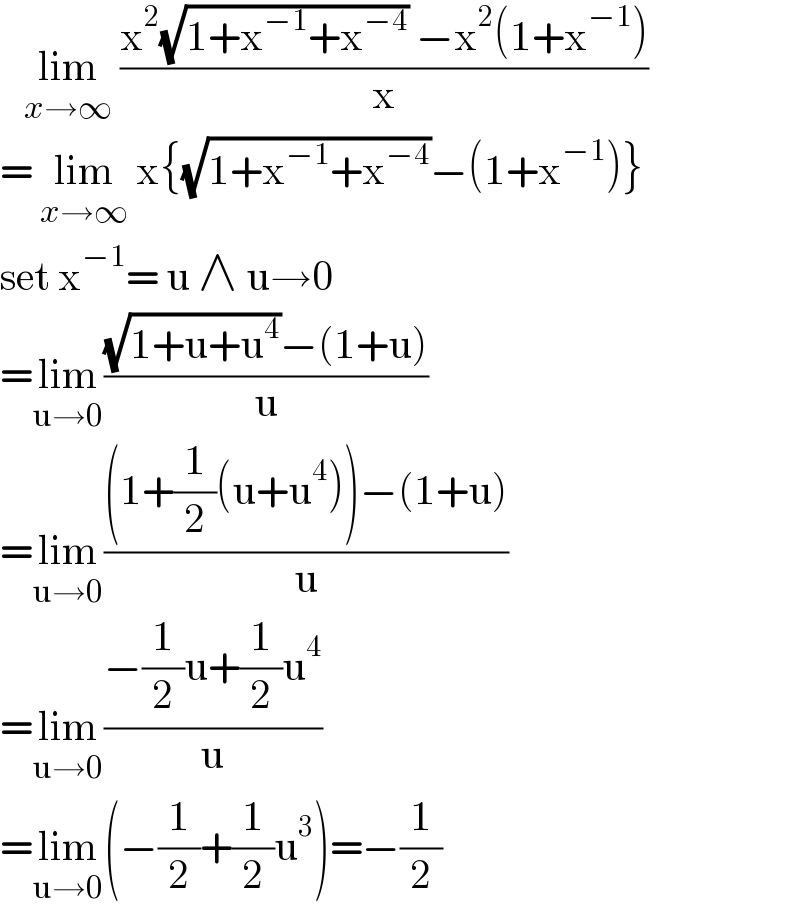
$$\:\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{x}^{\mathrm{2}} \sqrt{\mathrm{1}+\mathrm{x}^{−\mathrm{1}} +\mathrm{x}^{−\mathrm{4}} }\:−\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{x}^{−\mathrm{1}} \right)}{\mathrm{x}} \\ $$$$=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{x}\left\{\sqrt{\mathrm{1}+\mathrm{x}^{−\mathrm{1}} +\mathrm{x}^{−\mathrm{4}} }−\left(\mathrm{1}+\mathrm{x}^{−\mathrm{1}} \right)\right\} \\ $$$$\mathrm{set}\:\mathrm{x}^{−\mathrm{1}} =\:\mathrm{u}\:\wedge\:\mathrm{u}\rightarrow\mathrm{0} \\ $$$$=\underset{\mathrm{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt{\mathrm{1}+\mathrm{u}+\mathrm{u}^{\mathrm{4}} }−\left(\mathrm{1}+\mathrm{u}\right)}{\mathrm{u}} \\ $$$$=\underset{\mathrm{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{u}+\mathrm{u}^{\mathrm{4}} \right)\right)−\left(\mathrm{1}+\mathrm{u}\right)}{\mathrm{u}}\:\: \\ $$$$=\underset{\mathrm{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{u}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{u}^{\mathrm{4}} }{\mathrm{u}} \\ $$$$=\underset{\mathrm{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{u}^{\mathrm{3}} \right)=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by mnjuly1970 last updated on 06/Aug/21

$${thx}\:{alot}.. \\ $$
Answered by EDWIN88 last updated on 06/Aug/21

$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\left({x}^{\mathrm{4}} +{x}^{\mathrm{3}} +\mathrm{1}\right)−\left({x}^{\mathrm{2}} +{x}\right)^{\mathrm{2}} }{{x}\left(\sqrt{{x}^{\mathrm{4}} +{x}^{\mathrm{3}} +\mathrm{1}}\:+\left({x}+{x}^{\mathrm{2}} \right)\right)} \\ $$$$=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{{x}^{\mathrm{4}} +{x}^{\mathrm{3}} +\mathrm{1}−\left({x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{3}} +{x}^{\mathrm{2}} \right)}{{x}\left({x}^{\mathrm{2}} \sqrt{\mathrm{1}+\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{x}^{\mathrm{4}} }}+{x}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)\right)} \\ $$$$=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{−{x}^{\mathrm{3}} −{x}^{\mathrm{2}} +\mathrm{1}}{{x}^{\mathrm{3}} \left(\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{x}^{\mathrm{4}} }}+\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)} \\ $$$$=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{−\mathrm{1}−\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{x}^{\mathrm{3}} }}{\:\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{x}^{\mathrm{4}} }}+\mathrm{1}+\frac{\mathrm{1}}{{x}}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{1}}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by mnjuly1970 last updated on 06/Aug/21
$$\:\:{thank}\:{you}\:{so}\:{much}.. \\ $$
