Question Number 14965 by b.e.h.i.8.3.4.1.7@gmail.com last updated on 06/Jun/17

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 06/Jun/17

$${in}\:{triangle}\:{ABD}: \\ $$$${CF},{IH},{GJ},{are}\:{the}\:{perpendicular}\: \\ $$$${bisector}\:{of}\:{sides}. \\ $$$${AD}=\mathrm{12},{AB}=\mathrm{14},{BD}=\mathrm{16} \\ $$$$……………\sqrt{…….}….===\sqrt{……..}…=….. \\ $$$${S}_{{I}\overset{\Delta} {{K}J}} =?\:\:\:\:\:\:\left({S}={area}\right) \\ $$
Commented by ajfour last updated on 06/Jun/17

$${IJ}=\left({KC}\right)\left(\mathrm{tan}\:{A}+\mathrm{tan}\:{B}\right)\:. \\ $$
Answered by ajfour last updated on 06/Jun/17
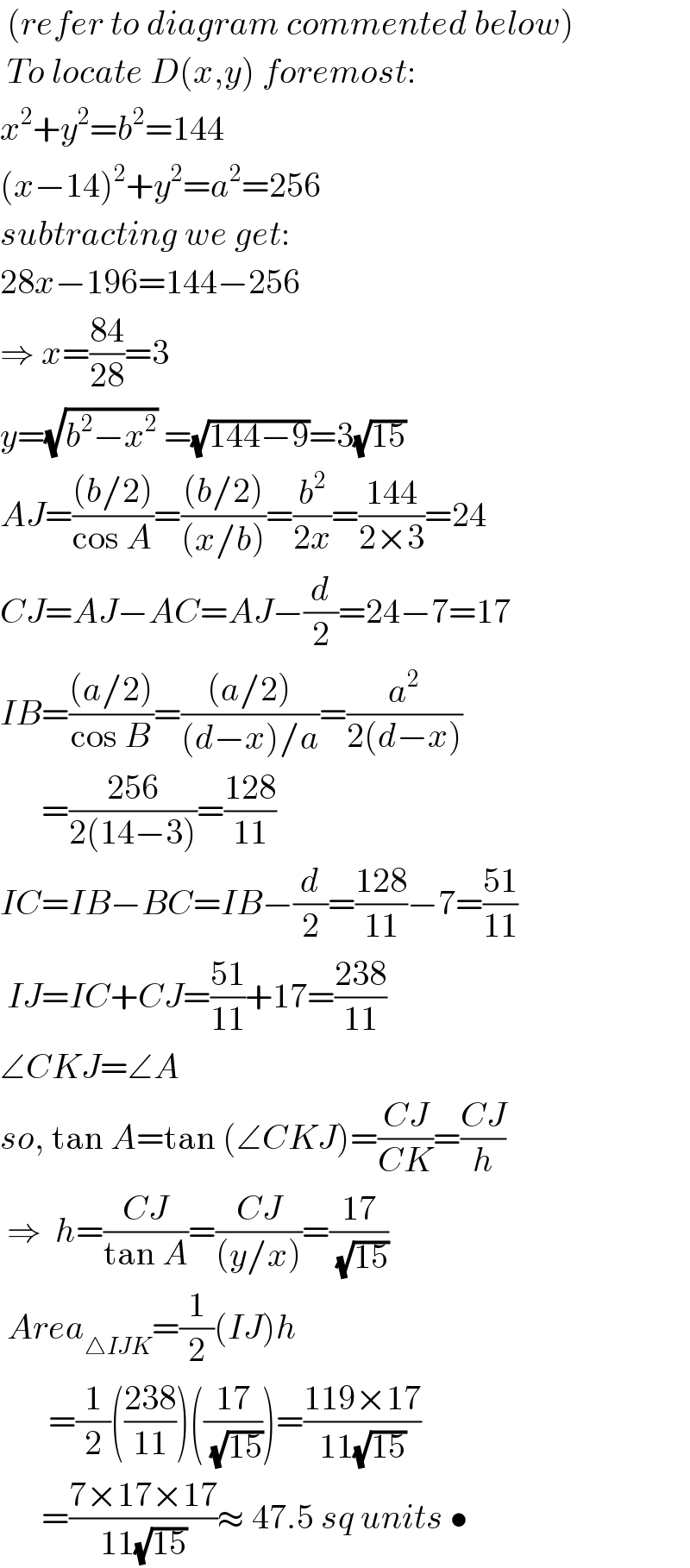
$$\:\left({refer}\:{to}\:{diagram}\:{commented}\:{below}\right) \\ $$$$\:{To}\:{locate}\:{D}\left({x},{y}\right)\:{foremost}: \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={b}^{\mathrm{2}} =\mathrm{144} \\ $$$$\left({x}−\mathrm{14}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} ={a}^{\mathrm{2}} =\mathrm{256} \\ $$$${subtracting}\:{we}\:{get}: \\ $$$$\mathrm{28}{x}−\mathrm{196}=\mathrm{144}−\mathrm{256} \\ $$$$\Rightarrow\:{x}=\frac{\mathrm{84}}{\mathrm{28}}=\mathrm{3} \\ $$$${y}=\sqrt{{b}^{\mathrm{2}} −{x}^{\mathrm{2}} }\:=\sqrt{\mathrm{144}−\mathrm{9}}=\mathrm{3}\sqrt{\mathrm{15}} \\ $$$${AJ}=\frac{\left({b}/\mathrm{2}\right)}{\mathrm{cos}\:{A}}=\frac{\left({b}/\mathrm{2}\right)}{\left({x}/{b}\right)}=\frac{{b}^{\mathrm{2}} }{\mathrm{2}{x}}=\frac{\mathrm{144}}{\mathrm{2}×\mathrm{3}}=\mathrm{24} \\ $$$${CJ}={AJ}−{AC}={AJ}−\frac{{d}}{\mathrm{2}}=\mathrm{24}−\mathrm{7}=\mathrm{17} \\ $$$${IB}=\frac{\left({a}/\mathrm{2}\right)}{\mathrm{cos}\:{B}}=\frac{\left({a}/\mathrm{2}\right)}{\left({d}−{x}\right)/{a}}=\frac{{a}^{\mathrm{2}} }{\mathrm{2}\left({d}−{x}\right)} \\ $$$$\:\:\:\:\:\:=\frac{\mathrm{256}}{\mathrm{2}\left(\mathrm{14}−\mathrm{3}\right)}=\frac{\mathrm{128}}{\mathrm{11}}\: \\ $$$${IC}={IB}−{BC}={IB}−\frac{{d}}{\mathrm{2}}=\frac{\mathrm{128}}{\mathrm{11}}−\mathrm{7}=\frac{\mathrm{51}}{\mathrm{11}} \\ $$$$\:{IJ}={IC}+{CJ}=\frac{\mathrm{51}}{\mathrm{11}}+\mathrm{17}=\frac{\mathrm{238}}{\mathrm{11}} \\ $$$$\angle{CKJ}=\angle{A} \\ $$$${so},\:\mathrm{tan}\:{A}=\mathrm{tan}\:\left(\angle{CKJ}\right)=\frac{{CJ}}{{CK}}=\frac{{CJ}}{{h}} \\ $$$$\:\Rightarrow\:\:{h}=\frac{{CJ}}{\mathrm{tan}\:{A}}=\frac{{CJ}}{\left({y}/{x}\right)}=\frac{\mathrm{17}}{\:\sqrt{\mathrm{15}}} \\ $$$$\:{Area}_{\bigtriangleup{IJK}} =\frac{\mathrm{1}}{\mathrm{2}}\left({IJ}\right){h} \\ $$$$\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{238}}{\mathrm{11}}\right)\left(\frac{\mathrm{17}}{\:\sqrt{\mathrm{15}}}\right)=\frac{\mathrm{119}×\mathrm{17}}{\mathrm{11}\sqrt{\mathrm{15}}} \\ $$$$\:\:\:\:\:\:=\frac{\mathrm{7}×\mathrm{17}×\mathrm{17}}{\mathrm{11}\sqrt{\mathrm{15}}}\approx\:\mathrm{47}.\mathrm{5}\:{sq}\:{units}\:\bullet \\ $$
Commented by ajfour last updated on 06/Jun/17

Commented by ajfour last updated on 06/Jun/17
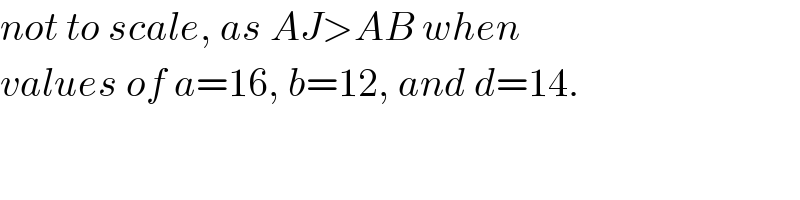
$${not}\:{to}\:{scale},\:{as}\:{AJ}>{AB}\:{when} \\ $$$${values}\:{of}\:{a}=\mathrm{16},\:{b}=\mathrm{12},\:{and}\:{d}=\mathrm{14}. \\ $$$$ \\ $$
Commented by RasheedSoomro last updated on 06/Jun/17

$$\mathcal{N}!\mathcal{CE}\:{approach}\:! \\ $$$$\mathcal{W}\mathrm{ithout}\:\mathrm{analytic}\:\mathrm{approach}\:\mathrm{it}\:\mathrm{will}\:\mathrm{be} \\ $$$$\mathrm{more}\:\mathrm{challenging}! \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 06/Jun/17
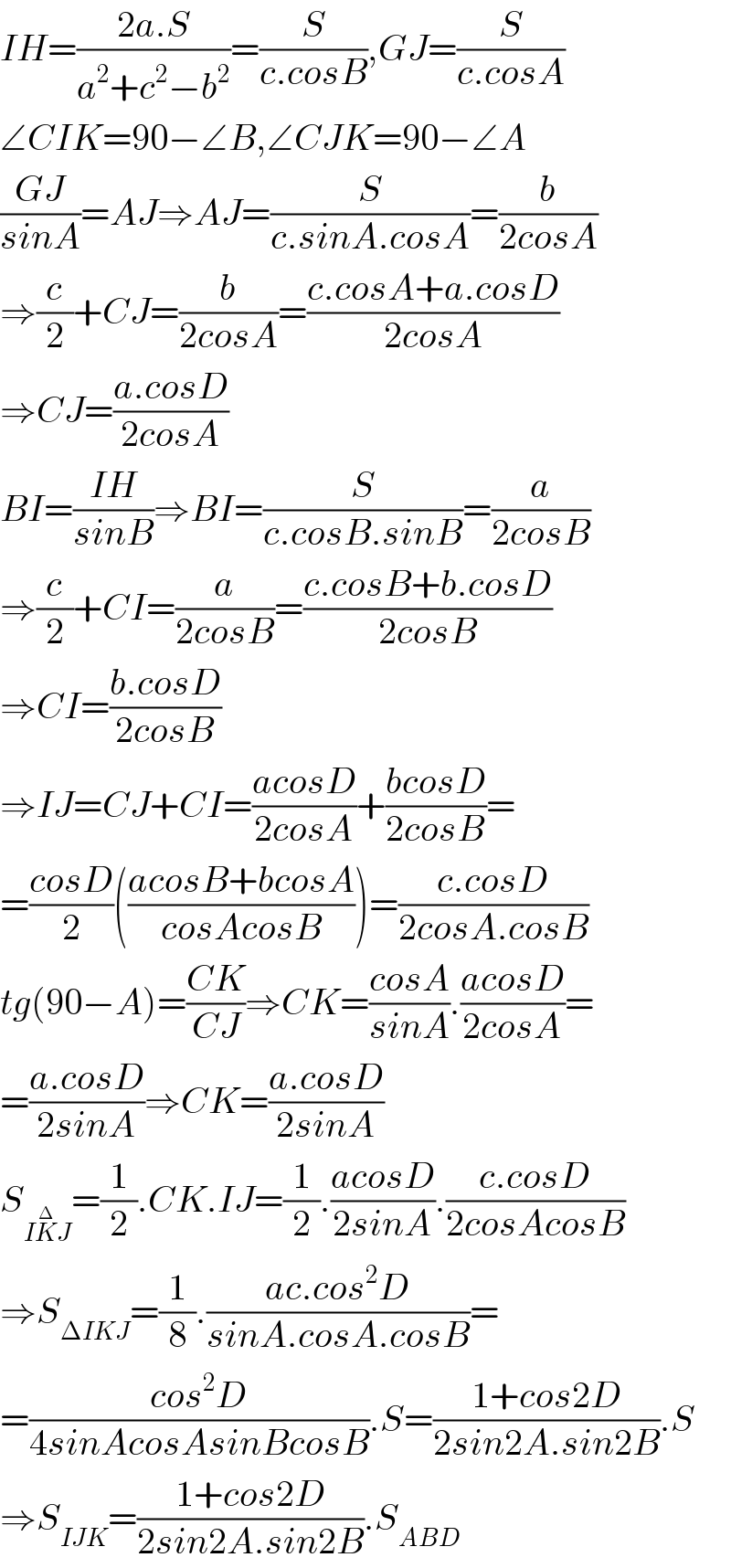
$${IH}=\frac{\mathrm{2}{a}.{S}}{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} −{b}^{\mathrm{2}} }=\frac{{S}}{{c}.{cosB}},{GJ}=\frac{{S}}{{c}.{cosA}} \\ $$$$\angle{CIK}=\mathrm{90}−\angle{B},\angle{CJK}=\mathrm{90}−\angle{A} \\ $$$$\frac{{GJ}}{{sinA}}={AJ}\Rightarrow{AJ}=\frac{{S}}{{c}.{sinA}.{cosA}}=\frac{{b}}{\mathrm{2}{cosA}} \\ $$$$\Rightarrow\frac{{c}}{\mathrm{2}}+{CJ}=\frac{{b}}{\mathrm{2}{cosA}}=\frac{{c}.{cosA}+{a}.{cosD}}{\mathrm{2}{cosA}} \\ $$$$\Rightarrow{CJ}=\frac{{a}.{cosD}}{\mathrm{2}{cosA}} \\ $$$${BI}=\frac{{IH}}{{sinB}}\Rightarrow{BI}=\frac{{S}}{{c}.{cosB}.{sinB}}=\frac{{a}}{\mathrm{2}{cosB}} \\ $$$$\Rightarrow\frac{{c}}{\mathrm{2}}+{CI}=\frac{{a}}{\mathrm{2}{cosB}}=\frac{{c}.{cosB}+{b}.{cosD}}{\mathrm{2}{cosB}} \\ $$$$\Rightarrow{CI}=\frac{{b}.{cosD}}{\mathrm{2}{cosB}} \\ $$$$\Rightarrow{IJ}={CJ}+{CI}=\frac{{acosD}}{\mathrm{2}{cosA}}+\frac{{bcosD}}{\mathrm{2}{cosB}}= \\ $$$$=\frac{{cosD}}{\mathrm{2}}\left(\frac{{acosB}+{bcosA}}{{cosAcosB}}\right)=\frac{{c}.{cosD}}{\mathrm{2}{cosA}.{cosB}} \\ $$$${tg}\left(\mathrm{90}−{A}\right)=\frac{{CK}}{{CJ}}\Rightarrow{CK}=\frac{{cosA}}{{sinA}}.\frac{{acosD}}{\mathrm{2}{cosA}}= \\ $$$$=\frac{{a}.{cosD}}{\mathrm{2}{sinA}}\Rightarrow{CK}=\frac{{a}.{cosD}}{\mathrm{2}{sinA}} \\ $$$${S}_{{I}\overset{\Delta} {{K}J}} =\frac{\mathrm{1}}{\mathrm{2}}.{CK}.{IJ}=\frac{\mathrm{1}}{\mathrm{2}}.\frac{{acosD}}{\mathrm{2}{sinA}}.\frac{{c}.{cosD}}{\mathrm{2}{cosAcosB}} \\ $$$$\Rightarrow{S}_{\Delta{IKJ}} =\frac{\mathrm{1}}{\mathrm{8}}.\frac{{ac}.{cos}^{\mathrm{2}} {D}}{{sinA}.{cosA}.{cosB}}= \\ $$$$=\frac{{cos}^{\mathrm{2}} {D}}{\mathrm{4}{sinAcosAsinBcosB}}.{S}=\frac{\mathrm{1}+{cos}\mathrm{2}{D}}{\mathrm{2}{sin}\mathrm{2}{A}.{sin}\mathrm{2}{B}}.{S} \\ $$$$\Rightarrow{S}_{{IJK}} =\frac{\mathrm{1}+{cos}\mathrm{2}{D}}{\mathrm{2}{sin}\mathrm{2}{A}.{sin}\mathrm{2}{B}}.{S}_{{ABD}} \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 06/Jun/17
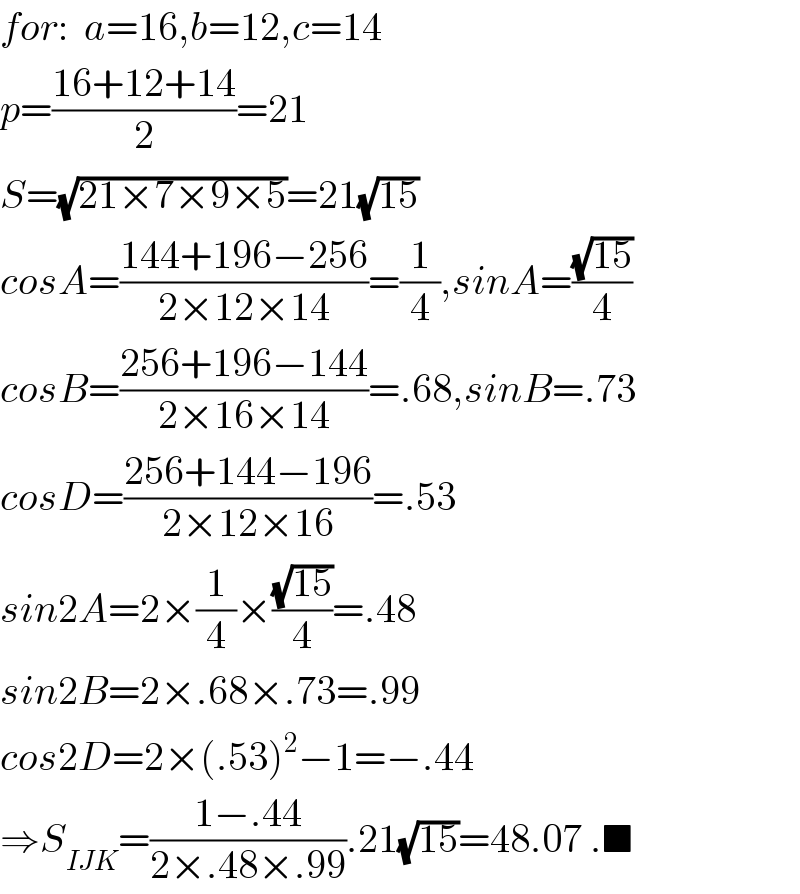
$${for}:\:\:{a}=\mathrm{16},{b}=\mathrm{12},{c}=\mathrm{14} \\ $$$${p}=\frac{\mathrm{16}+\mathrm{12}+\mathrm{14}}{\mathrm{2}}=\mathrm{21} \\ $$$${S}=\sqrt{\mathrm{21}×\mathrm{7}×\mathrm{9}×\mathrm{5}}=\mathrm{21}\sqrt{\mathrm{15}} \\ $$$${cosA}=\frac{\mathrm{144}+\mathrm{196}−\mathrm{256}}{\mathrm{2}×\mathrm{12}×\mathrm{14}}=\frac{\mathrm{1}}{\mathrm{4}},{sinA}=\frac{\sqrt{\mathrm{15}}}{\mathrm{4}} \\ $$$${cosB}=\frac{\mathrm{256}+\mathrm{196}−\mathrm{144}}{\mathrm{2}×\mathrm{16}×\mathrm{14}}=.\mathrm{68},{sinB}=.\mathrm{73} \\ $$$${cosD}=\frac{\mathrm{256}+\mathrm{144}−\mathrm{196}}{\mathrm{2}×\mathrm{12}×\mathrm{16}}=.\mathrm{53} \\ $$$${sin}\mathrm{2}{A}=\mathrm{2}×\frac{\mathrm{1}}{\mathrm{4}}×\frac{\sqrt{\mathrm{15}}}{\mathrm{4}}=.\mathrm{48} \\ $$$${sin}\mathrm{2}{B}=\mathrm{2}×.\mathrm{68}×.\mathrm{73}=.\mathrm{99} \\ $$$${cos}\mathrm{2}{D}=\mathrm{2}×\left(.\mathrm{53}\right)^{\mathrm{2}} −\mathrm{1}=−.\mathrm{44} \\ $$$$\Rightarrow{S}_{{IJK}} =\frac{\mathrm{1}−.\mathrm{44}}{\mathrm{2}×.\mathrm{48}×.\mathrm{99}}.\mathrm{21}\sqrt{\mathrm{15}}=\mathrm{48}.\mathrm{07}\:.\blacksquare \\ $$
