Question Number 149718 by peter frank last updated on 06/Aug/21
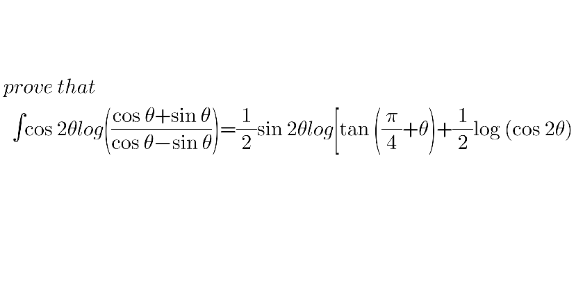
Answered by Ar Brandon last updated on 06/Aug/21
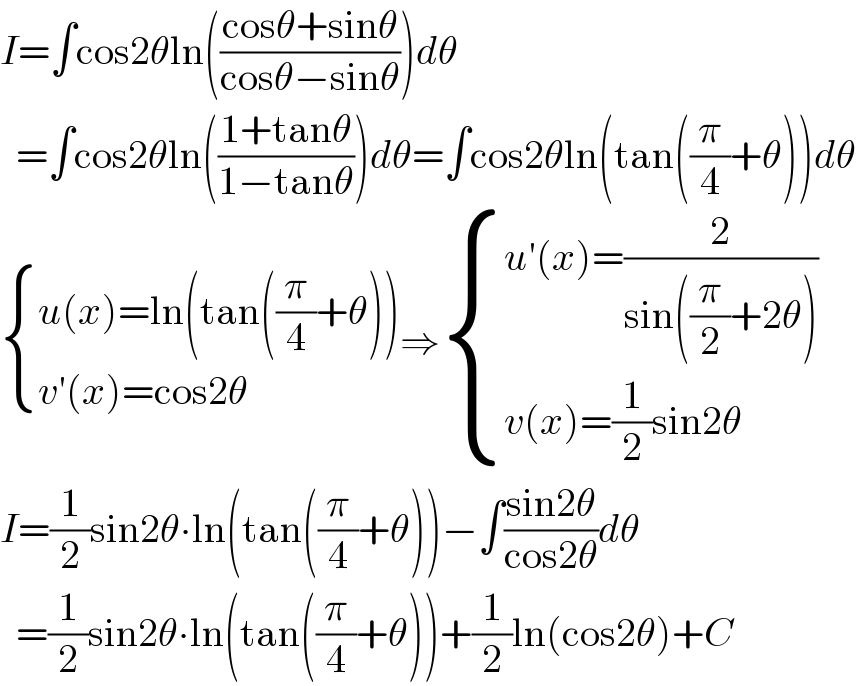
$${I}=\int\mathrm{cos2}\theta\mathrm{ln}\left(\frac{\mathrm{cos}\theta+\mathrm{sin}\theta}{\mathrm{cos}\theta−\mathrm{sin}\theta}\right){d}\theta \\ $$$$\:\:=\int\mathrm{cos2}\theta\mathrm{ln}\left(\frac{\mathrm{1}+\mathrm{tan}\theta}{\mathrm{1}−\mathrm{tan}\theta}\right){d}\theta=\int\mathrm{cos2}\theta\mathrm{ln}\left(\mathrm{tan}\left(\frac{\pi}{\mathrm{4}}+\theta\right)\right){d}\theta \\ $$$$\begin{cases}{{u}\left({x}\right)=\mathrm{ln}\left(\mathrm{tan}\left(\frac{\pi}{\mathrm{4}}+\theta\right)\right)}\\{{v}'\left({x}\right)=\mathrm{cos2}\theta}\end{cases}\Rightarrow\begin{cases}{{u}'\left({x}\right)=\frac{\mathrm{2}}{\mathrm{sin}\left(\frac{\pi}{\mathrm{2}}+\mathrm{2}\theta\right)}}\\{{v}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin2}\theta}\end{cases} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin2}\theta\centerdot\mathrm{ln}\left(\mathrm{tan}\left(\frac{\pi}{\mathrm{4}}+\theta\right)\right)−\int\frac{\mathrm{sin2}\theta}{\mathrm{cos2}\theta}{d}\theta \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin2}\theta\centerdot\mathrm{ln}\left(\mathrm{tan}\left(\frac{\pi}{\mathrm{4}}+\theta\right)\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{cos2}\theta\right)+{C} \\ $$
