Menu Close

Question-149739

Tinku Tara 0 Comments
Pin




Question Number 149739 by iloveisrael last updated on 07/Aug/21
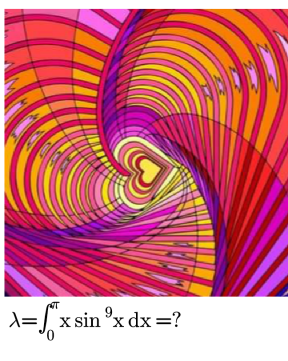
Answered by Olaf_Thorendsen last updated on 07/Aug/21
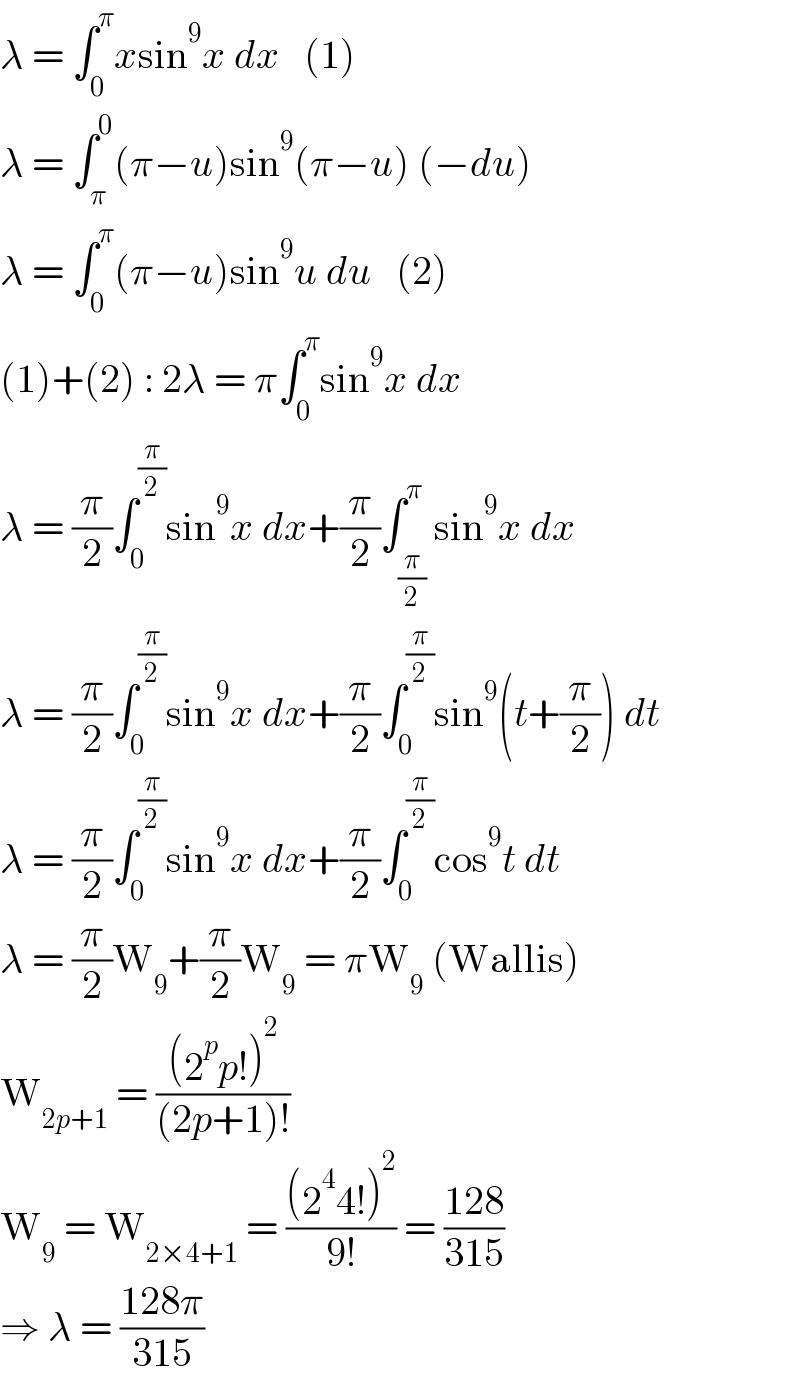
λ = ∫_0 ^π xsin^9 x dx (1) λ = ∫_π ^0 (π−u)sin^9 (π−u) (−du) λ = ∫_0 ^π (π−u)sin^9 u du (2) (1)+(2) : 2λ = π∫_0 ^π sin^9 x dx λ = (π/2)∫_0 ^(π/2) sin^9 x dx+(π/2)∫_(π/2) ^π sin^9 x dx λ = (π/2)∫_0 ^(π/2) sin^9 x dx+(π/2)∫_0 ^(π/2) sin^9 (t+(π/2)) dt λ = (π/2)∫_0 ^(π/2) sin^9 x dx+(π/2)∫_0 ^(π/2) cos^9 t dt λ = (π/2)W_9 +(π/2)W_9 = πW_9 (Wallis) W_(2p+1) = (((2^p p!)^2 )/((2p+1)!)) W_9 = W_(2×4+1) = (((2^4 4!)^2 )/(9!)) = ((128)/(315)) ⇒ λ = ((128π)/(315))
$$\lambda\:=\:\int_{\mathrm{0}} ^{\pi} {x}\mathrm{sin}^{\mathrm{9}} {x}\:{dx}\:\:\:\left(\mathrm{1}\right) \\ $$$$\lambda\:=\:\int_{\pi} ^{\mathrm{0}} \left(\pi−{u}\right)\mathrm{sin}^{\mathrm{9}} \left(\pi−{u}\right)\:\left(−{du}\right) \\ $$$$\lambda\:=\:\int_{\mathrm{0}} ^{\pi} \left(\pi−{u}\right)\mathrm{sin}^{\mathrm{9}} {u}\:{du}\:\:\:\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)+\left(\mathrm{2}\right)\::\:\mathrm{2}\lambda\:=\:\pi\int_{\mathrm{0}} ^{\pi} \mathrm{sin}^{\mathrm{9}} {x}\:{dx} \\ $$$$\lambda\:=\:\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{9}} {x}\:{dx}+\frac{\pi}{\mathrm{2}}\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} \mathrm{sin}^{\mathrm{9}} {x}\:{dx} \\ $$$$\lambda\:=\:\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{9}} {x}\:{dx}+\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{9}} \left({t}+\frac{\pi}{\mathrm{2}}\right)\:{dt} \\ $$$$\lambda\:=\:\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{9}} {x}\:{dx}+\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cos}^{\mathrm{9}} {t}\:{dt} \\ $$$$\lambda\:=\:\frac{\pi}{\mathrm{2}}\mathrm{W}_{\mathrm{9}} +\frac{\pi}{\mathrm{2}}\mathrm{W}_{\mathrm{9}} \:=\:\pi\mathrm{W}_{\mathrm{9}} \:\left(\mathrm{Wallis}\right) \\ $$$$\mathrm{W}_{\mathrm{2}{p}+\mathrm{1}} \:=\:\frac{\left(\mathrm{2}^{{p}} {p}!\right)^{\mathrm{2}} }{\left(\mathrm{2}{p}+\mathrm{1}\right)!} \\ $$$$\mathrm{W}_{\mathrm{9}} \:=\:\mathrm{W}_{\mathrm{2}×\mathrm{4}+\mathrm{1}} \:=\:\frac{\left(\mathrm{2}^{\mathrm{4}} \mathrm{4}!\right)^{\mathrm{2}} }{\mathrm{9}!}\:=\:\frac{\mathrm{128}}{\mathrm{315}} \\ $$$$\Rightarrow\:\lambda\:=\:\frac{\mathrm{128}\pi}{\mathrm{315}} \\ $$
Answered by mathmax by abdo last updated on 07/Aug/21
Ψ=∫_0 ^π x sin^9 x dx ⇒Ψ=∫_0 ^π x(((e^(ix) −e^(−ix) )/(2i)))^9 dx =(1/((2i)^9 ))∫_0 ^π x(Σ_(k=0) ^9 C_9 ^k (e^(ix) )^k (−e^(−ix) )^(9−k) )dx =(1/((2i)^9 ))Σ_(k=0) ^9 C_9 ^k (−1)^(9−k) ∫_0 ^π x e^(ikx) e^((k−9)ix) dx =−(1/((2i)^9 ))Σ_(k=0) ^9 (−1)^k C_9 ^k u_k u_k =∫_0 ^π x e^((2k−9)ix) dx =[(x/((2k−9)i))e^((2k−9)ix) ]_0 ^π −∫_0 ^π (1/((2k−9)i))e^((2k−9)ix) dx =(π/((2k−9)i))e^((2k−9)iπ) −(1/(((2k−9)i)^2 ))[e^((2k−9)ix) ]_0 ^π =−(π/((2k−9)i))+(1/((2k−9)^2 ))(−2) ⇒ Ψ=−(1/((2i)^9 ))Σ_(k=0) ^9 (−1)^k C_9 ^k (−(π/((2k−9)i))−(2/((2k−9)^2 )))....
$$\Psi=\int_{\mathrm{0}} ^{\pi} \:\mathrm{x}\:\mathrm{sin}^{\mathrm{9}} \mathrm{x}\:\mathrm{dx}\:\Rightarrow\Psi=\int_{\mathrm{0}} ^{\pi} \:\mathrm{x}\left(\frac{\mathrm{e}^{\mathrm{ix}} −\mathrm{e}^{−\mathrm{ix}} }{\mathrm{2i}}\right)^{\mathrm{9}} \:\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{2i}\right)^{\mathrm{9}} }\int_{\mathrm{0}} ^{\pi} \mathrm{x}\left(\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{9}} \:\mathrm{C}_{\mathrm{9}} ^{\mathrm{k}} \:\left(\mathrm{e}^{\mathrm{ix}} \right)^{\mathrm{k}} \left(−\mathrm{e}^{−\mathrm{ix}} \right)^{\mathrm{9}−\mathrm{k}} \right)\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{2i}\right)^{\mathrm{9}} }\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{9}} \:\mathrm{C}_{\mathrm{9}} ^{\mathrm{k}} \left(−\mathrm{1}\right)^{\mathrm{9}−\mathrm{k}} \:\int_{\mathrm{0}} ^{\pi} \mathrm{x}\:\mathrm{e}^{\mathrm{ikx}} \:\mathrm{e}^{\left(\mathrm{k}−\mathrm{9}\right)\mathrm{ix}} \mathrm{dx} \\ $$$$=−\frac{\mathrm{1}}{\left(\mathrm{2i}\right)^{\mathrm{9}} }\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{9}} \:\left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{9}} ^{\mathrm{k}} \:\mathrm{u}_{\mathrm{k}} \\ $$$$\mathrm{u}_{\mathrm{k}} =\int_{\mathrm{0}} ^{\pi} \mathrm{x}\:\mathrm{e}^{\left(\mathrm{2k}−\mathrm{9}\right)\mathrm{ix}} \:\mathrm{dx}\:=\left[\frac{\mathrm{x}}{\left(\mathrm{2k}−\mathrm{9}\right)\mathrm{i}}\mathrm{e}^{\left(\mathrm{2k}−\mathrm{9}\right)\mathrm{ix}} \right]_{\mathrm{0}} ^{\pi} −\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{1}}{\left(\mathrm{2k}−\mathrm{9}\right)\mathrm{i}}\mathrm{e}^{\left(\mathrm{2k}−\mathrm{9}\right)\mathrm{ix}} \mathrm{dx} \\ $$$$=\frac{\pi}{\left(\mathrm{2k}−\mathrm{9}\right)\mathrm{i}}\mathrm{e}^{\left(\mathrm{2k}−\mathrm{9}\right)\mathrm{i}\pi} \:−\frac{\mathrm{1}}{\left(\left(\mathrm{2k}−\mathrm{9}\right)\mathrm{i}\right)^{\mathrm{2}} }\left[\mathrm{e}^{\left(\mathrm{2k}−\mathrm{9}\right)\mathrm{ix}} \right]_{\mathrm{0}} ^{\pi} \\ $$$$=−\frac{\pi}{\left(\mathrm{2k}−\mathrm{9}\right)\mathrm{i}}+\frac{\mathrm{1}}{\left(\mathrm{2k}−\mathrm{9}\right)^{\mathrm{2}} }\left(−\mathrm{2}\right)\:\Rightarrow \\ $$$$\Psi=−\frac{\mathrm{1}}{\left(\mathrm{2i}\right)^{\mathrm{9}} }\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{9}} \left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{9}} ^{\mathrm{k}} \left(−\frac{\pi}{\left(\mathrm{2k}−\mathrm{9}\right)\mathrm{i}}−\frac{\mathrm{2}}{\left(\mathrm{2k}−\mathrm{9}\right)^{\mathrm{2}} }\right)…. \\ $$
Answered by gsk2684 last updated on 07/Aug/21
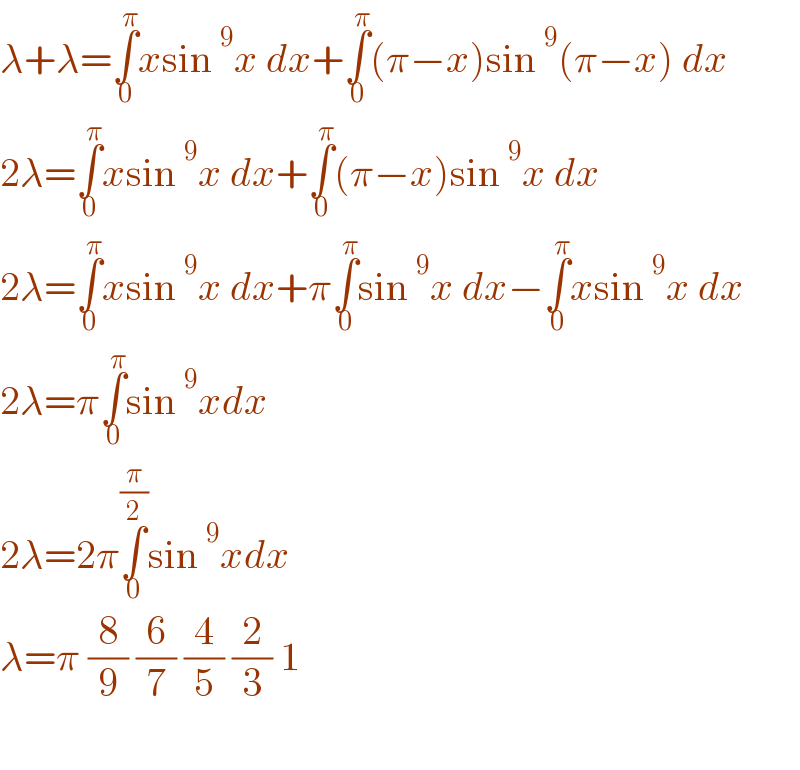
λ+λ=∫_0 ^π xsin^9 x dx+∫_0 ^π (π−x)sin^9 (π−x) dx 2λ=∫_0 ^π xsin^9 x dx+∫_0 ^π (π−x)sin^9 x dx 2λ=∫_0 ^π xsin^9 x dx+π∫_0 ^π sin^9 x dx−∫_0 ^π xsin^9 x dx 2λ=π∫_0 ^π sin^9 xdx 2λ=2π∫_0 ^(π/2) sin^9 xdx λ=π (8/9) (6/7) (4/5) (2/3) 1
$$\lambda+\lambda=\underset{\mathrm{0}} {\overset{\pi} {\int}}{x}\mathrm{sin}\:^{\mathrm{9}} {x}\:{dx}+\underset{\mathrm{0}} {\overset{\pi} {\int}}\left(\pi−{x}\right)\mathrm{sin}\:^{\mathrm{9}} \left(\pi−{x}\right)\:{dx} \\ $$$$\mathrm{2}\lambda=\underset{\mathrm{0}} {\overset{\pi} {\int}}{x}\mathrm{sin}\:^{\mathrm{9}} {x}\:{dx}+\underset{\mathrm{0}} {\overset{\pi} {\int}}\left(\pi−{x}\right)\mathrm{sin}\:^{\mathrm{9}} {x}\:{dx} \\ $$$$\mathrm{2}\lambda=\underset{\mathrm{0}} {\overset{\pi} {\int}}{x}\mathrm{sin}\:^{\mathrm{9}} {x}\:{dx}+\pi\underset{\mathrm{0}} {\overset{\pi} {\int}}\mathrm{sin}\:^{\mathrm{9}} {x}\:{dx}−\underset{\mathrm{0}} {\overset{\pi} {\int}}{x}\mathrm{sin}\:^{\mathrm{9}} {x}\:{dx} \\ $$$$\mathrm{2}\lambda=\pi\underset{\mathrm{0}} {\overset{\pi} {\int}}\mathrm{sin}\:^{\mathrm{9}} {xdx} \\ $$$$\mathrm{2}\lambda=\mathrm{2}\pi\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\mathrm{sin}\:^{\mathrm{9}} {xdx} \\ $$$$\lambda=\pi\:\frac{\mathrm{8}}{\mathrm{9}}\:\frac{\mathrm{6}}{\mathrm{7}}\:\frac{\mathrm{4}}{\mathrm{5}}\:\frac{\mathrm{2}}{\mathrm{3}}\:\mathrm{1} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *