Question Number 149773 by Samimsultani last updated on 07/Aug/21
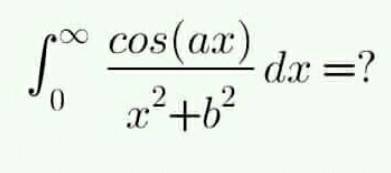
Answered by puissant last updated on 07/Aug/21

$${I}=\int_{\mathrm{0}} ^{\infty} \frac{{cos}\left({ax}\right)}{{x}^{\mathrm{2}} +{b}^{\mathrm{2}} }{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{+\infty} \frac{{cos}\left({ax}\right)}{{x}^{\mathrm{2}} +{b}^{\mathrm{2}} }{dx}\:\:{car}\:{cos}\left({x}\right)\:{est}\:{paire} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{Re}\left(\int_{−\infty} ^{+\infty} \frac{{e}^{{aix}} }{{x}^{\mathrm{2}} +{b}^{\mathrm{2}} }{dx}\right) \\ $$$${or}\:\psi=\int_{−\infty} ^{+\infty} \frac{{e}^{{iax}} }{{x}^{\mathrm{2}} +{b}^{\mathrm{2}} }{dx}\:=\:\mathrm{2}{i}\pi\:{Res}\left(\psi,{ib}\right) \\ $$$$\left({theoreme}\:{du}\:{residu}.\right).. \\ $$$$=\mathrm{2}{i}\pi\frac{{e}^{{ia}\left({ib}\right)} }{\mathrm{2}{ib}} \\ $$$$=\frac{\pi}{{b}}{e}^{−{ab}} \\ $$$${d}'{ou}\:\:\:\because\:\:\:\:\:{I}=\frac{\pi}{\mathrm{2}{b}}{e}^{−{ab}} …. \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:….{Le}\:{puissant}…. \\ $$
