Menu Close

Question-149854

Tinku Tara 0 Comments
Pin




Question Number 149854 by mathdanisur last updated on 07/Aug/21
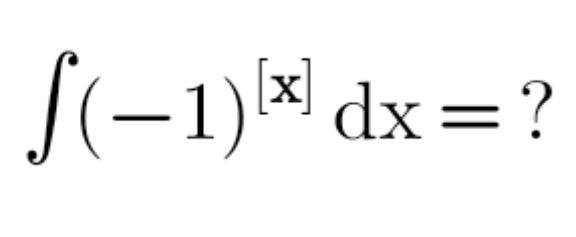
Commented by mr W last updated on 08/Aug/21
i gave an answer. you didn′t agree, but gave an other answer which is in fact the same as my answer.
$${i}\:{gave}\:{an}\:{answer}.\:{you}\:{didn}'{t}\:{agree}, \\ $$$${but}\:{gave}\:{an}\:{other}\:{answer}\:{which} \\ $$$${is}\:{in}\:{fact}\:{the}\:{same}\:{as}\:{my}\:{answer}. \\ $$
Commented by mr W last updated on 08/Aug/21
you said it is zero, not i.
$${you}\:{said}\:{it}\:{is}\:{zero},\:{not}\:{i}. \\ $$
Commented by mr W last updated on 07/Aug/21
= { ((x+C if [x] is even)),((−x+C if [x] is odd)) :}
$$=\begin{cases}{{x}+{C}\:{if}\:\left[{x}\right]\:{is}\:{even}}\\{−{x}+{C}\:{if}\:\left[{x}\right]\:{is}\:{odd}}\end{cases} \\ $$
Commented by mathdanisur last updated on 08/Aug/21
Thanks Ser, but answer periodik
$$\mathrm{Thanks}\:\mathrm{Ser},\:\mathrm{but}\:\mathrm{answer}\:\mathrm{periodik} \\ $$
Commented by mr W last updated on 08/Aug/21
please tell what concretely is not correct. when i say if [x] is even, it is the same as to say if 0≤x<1, 2≤x<3, 4≤x<5, ... and when i say if [x] is odd, it is the same as to say if 1≤x<2, 3≤x<4, 5≤x<6, ...
$${please}\:{tell}\:{what}\:{concretely}\:{is}\:{not} \\ $$$${correct}.\:{when}\:{i}\:{say}\:{if}\:\left[{x}\right]\:{is}\:{even}, \\ $$$${it}\:{is}\:{the}\:{same}\:{as}\:{to}\:{say}\:{if}\:\mathrm{0}\leqslant{x}<\mathrm{1}, \\ $$$$\mathrm{2}\leqslant{x}<\mathrm{3},\:\mathrm{4}\leqslant{x}<\mathrm{5},\:… \\ $$$${and}\:{when}\:{i}\:{say}\:{if}\:\left[{x}\right]\:{is}\:{odd},\:{it}\:{is}\:{the} \\ $$$${same}\:{as}\:{to}\:{say}\:{if}\:\mathrm{1}\leqslant{x}<\mathrm{2},\:\mathrm{3}\leqslant{x}<\mathrm{4}, \\ $$$$\mathrm{5}\leqslant{x}<\mathrm{6},\:… \\ $$
Commented by mathdanisur last updated on 08/Aug/21
x+C [x] even −x+C[x] odd Ser but your answer here is zero.?
$${x}+{C}\:\left[{x}\right]\:{even} \\ $$$$−{x}+{C}\left[{x}\right]\:{odd} \\ $$$${Ser}\:{but}\:{your}\:{answer}\:{here}\:{is}\:{zero}.? \\ $$
Commented by mathdanisur last updated on 08/Aug/21
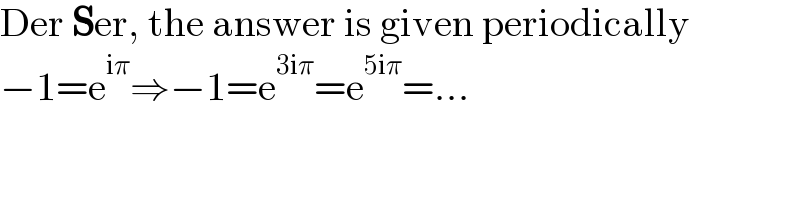
Der Ser, the answer is given periodically −1=e^(iπ) ⇒−1=e^(3iπ) =e^(5iπ) =...
$$\mathrm{Der}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{given}\:\mathrm{periodically} \\ $$$$−\mathrm{1}=\mathrm{e}^{\mathrm{i}\pi} \Rightarrow−\mathrm{1}=\mathrm{e}^{\mathrm{3i}\pi} =\mathrm{e}^{\mathrm{5i}\pi} =… \\ $$
Commented by mr W last updated on 08/Aug/21
i don′t understand that, too high to me. you even didn′t tell what the concrete answer is.
$${i}\:{don}'{t}\:{understand}\:{that},\:{too}\:{high}\:{to}\:{me}. \\ $$$${you}\:{even}\:{didn}'{t}\:{tell}\:{what}\:{the}\:{concrete} \\ $$$${answer}\:{is}. \\ $$
Commented by mathdanisur last updated on 08/Aug/21
Ser, answer: ∫(−1)^([x]) dx = (1/π) arccos(cosπx)+C
$$\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{answer}:\:\int\left(−\mathrm{1}\right)^{\left[\boldsymbol{\mathrm{x}}\right]} \mathrm{dx}\:=\:\frac{\mathrm{1}}{\pi}\:\mathrm{arccos}\left(\mathrm{cos}\pi\mathrm{x}\right)+\mathrm{C} \\ $$
Commented by mr W last updated on 08/Aug/21
don′t you see that this is absolutely the same as my answer? ((cos^(−1) (πx))/π)=x if 2k≤x<2k+1 ((cos^(−1) (πx))/π)=−x if 2k+1≤x<2k+2
$${don}'{t}\:{you}\:{see}\:{that}\:{this}\:{is}\:{absolutely} \\ $$$${the}\:{same}\:{as}\:{my}\:{answer}? \\ $$$$\frac{\mathrm{cos}^{−\mathrm{1}} \left(\pi{x}\right)}{\pi}={x}\:{if}\:\mathrm{2}{k}\leqslant{x}<\mathrm{2}{k}+\mathrm{1} \\ $$$$\frac{\mathrm{cos}^{−\mathrm{1}} \left(\pi{x}\right)}{\pi}=−{x}\:{if}\:\mathrm{2}{k}+\mathrm{1}\leqslant{x}<\mathrm{2}{k}+\mathrm{2} \\ $$
Commented by mathdanisur last updated on 08/Aug/21
Very nice Ser thankyou
$$\mathrm{Very}\:\mathrm{nice}\:\boldsymbol{\mathrm{S}}\mathrm{er}\:\mathrm{thankyou} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *