Question Number 149889 by Samimsultani last updated on 08/Aug/21
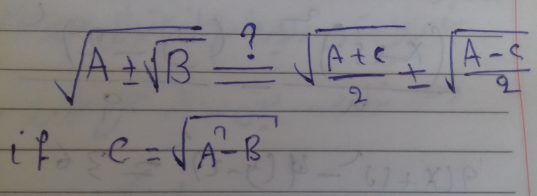
Commented by bramlexs22 last updated on 08/Aug/21
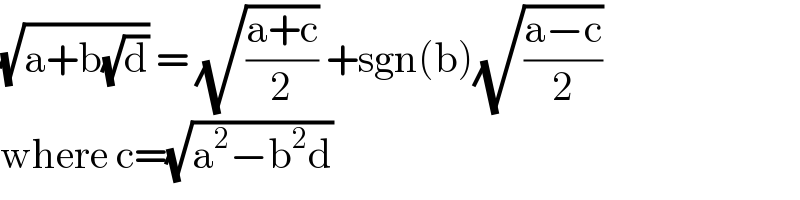
$$\sqrt{\mathrm{a}+\mathrm{b}\sqrt{\mathrm{d}}}\:=\:\sqrt{\frac{\mathrm{a}+\mathrm{c}}{\mathrm{2}}}\:+\mathrm{sgn}\left(\mathrm{b}\right)\sqrt{\frac{\mathrm{a}−\mathrm{c}}{\mathrm{2}}} \\ $$$$\mathrm{where}\:\mathrm{c}=\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \mathrm{d}}\: \\ $$
Commented by Samimsultani last updated on 08/Aug/21

$$ \\ $$$$\:\:{please}\:{proof}??? \\ $$
Commented by bramlexs22 last updated on 08/Aug/21
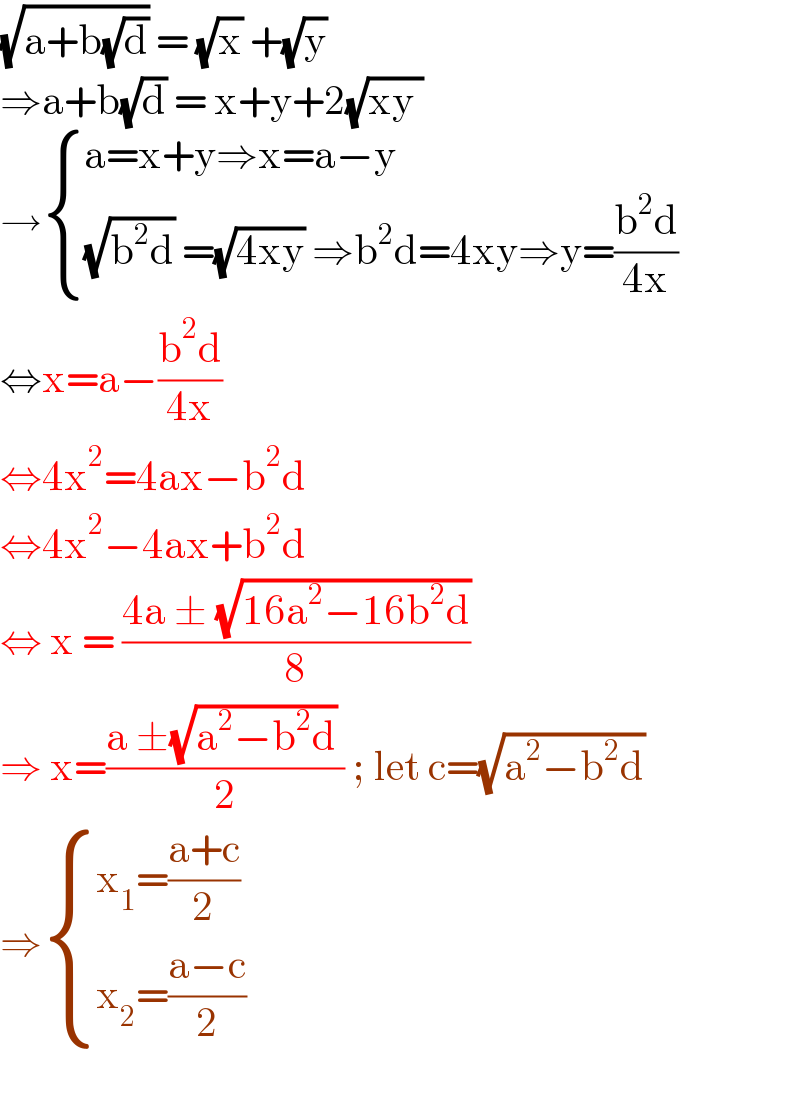
$$\sqrt{\mathrm{a}+\mathrm{b}\sqrt{\mathrm{d}}}\:=\:\sqrt{\mathrm{x}}\:+\sqrt{\mathrm{y}} \\ $$$$\Rightarrow\mathrm{a}+\mathrm{b}\sqrt{\mathrm{d}}\:=\:\mathrm{x}+\mathrm{y}+\mathrm{2}\sqrt{\mathrm{xy}\:} \\ $$$$\rightarrow\begin{cases}{\mathrm{a}=\mathrm{x}+\mathrm{y}\Rightarrow\mathrm{x}=\mathrm{a}−\mathrm{y}}\\{\sqrt{\mathrm{b}^{\mathrm{2}} \mathrm{d}}\:=\sqrt{\mathrm{4xy}}\:\Rightarrow\mathrm{b}^{\mathrm{2}} \mathrm{d}=\mathrm{4xy}\Rightarrow\mathrm{y}=\frac{\mathrm{b}^{\mathrm{2}} \mathrm{d}}{\mathrm{4x}}}\end{cases} \\ $$$$\Leftrightarrow\mathrm{x}=\mathrm{a}−\frac{\mathrm{b}^{\mathrm{2}} \mathrm{d}}{\mathrm{4x}} \\ $$$$\Leftrightarrow\mathrm{4x}^{\mathrm{2}} =\mathrm{4ax}−\mathrm{b}^{\mathrm{2}} \mathrm{d} \\ $$$$\Leftrightarrow\mathrm{4x}^{\mathrm{2}} −\mathrm{4ax}+\mathrm{b}^{\mathrm{2}} \mathrm{d}\: \\ $$$$\Leftrightarrow\:\mathrm{x}\:=\:\frac{\mathrm{4a}\:\pm\:\sqrt{\mathrm{16a}^{\mathrm{2}} −\mathrm{16b}^{\mathrm{2}} \mathrm{d}}}{\mathrm{8}} \\ $$$$\Rightarrow\:\mathrm{x}=\frac{\mathrm{a}\:\pm\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \mathrm{d}}\:}{\mathrm{2}}\:;\:\mathrm{let}\:\mathrm{c}=\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \mathrm{d}} \\ $$$$\Rightarrow\begin{cases}{\mathrm{x}_{\mathrm{1}} =\frac{\mathrm{a}+\mathrm{c}}{\mathrm{2}}}\\{\mathrm{x}_{\mathrm{2}} =\frac{\mathrm{a}−\mathrm{c}}{\mathrm{2}}}\end{cases} \\ $$$$ \\ $$
