Question-149894

Question Number 149894 by ajfour last updated on 08/Aug/21

Commented by ajfour last updated on 08/Aug/21

$${Find}\:{minimum}\:{and}\:{maximum} \\ $$$${values}\:{for}\:{the}\:{side}\:{of}\:{equilateral} \\ $$$${triangle}\:{shown}. \\ $$

Answered by mr W last updated on 08/Aug/21

Commented by mr W last updated on 08/Aug/21

Commented by mr W last updated on 08/Aug/21

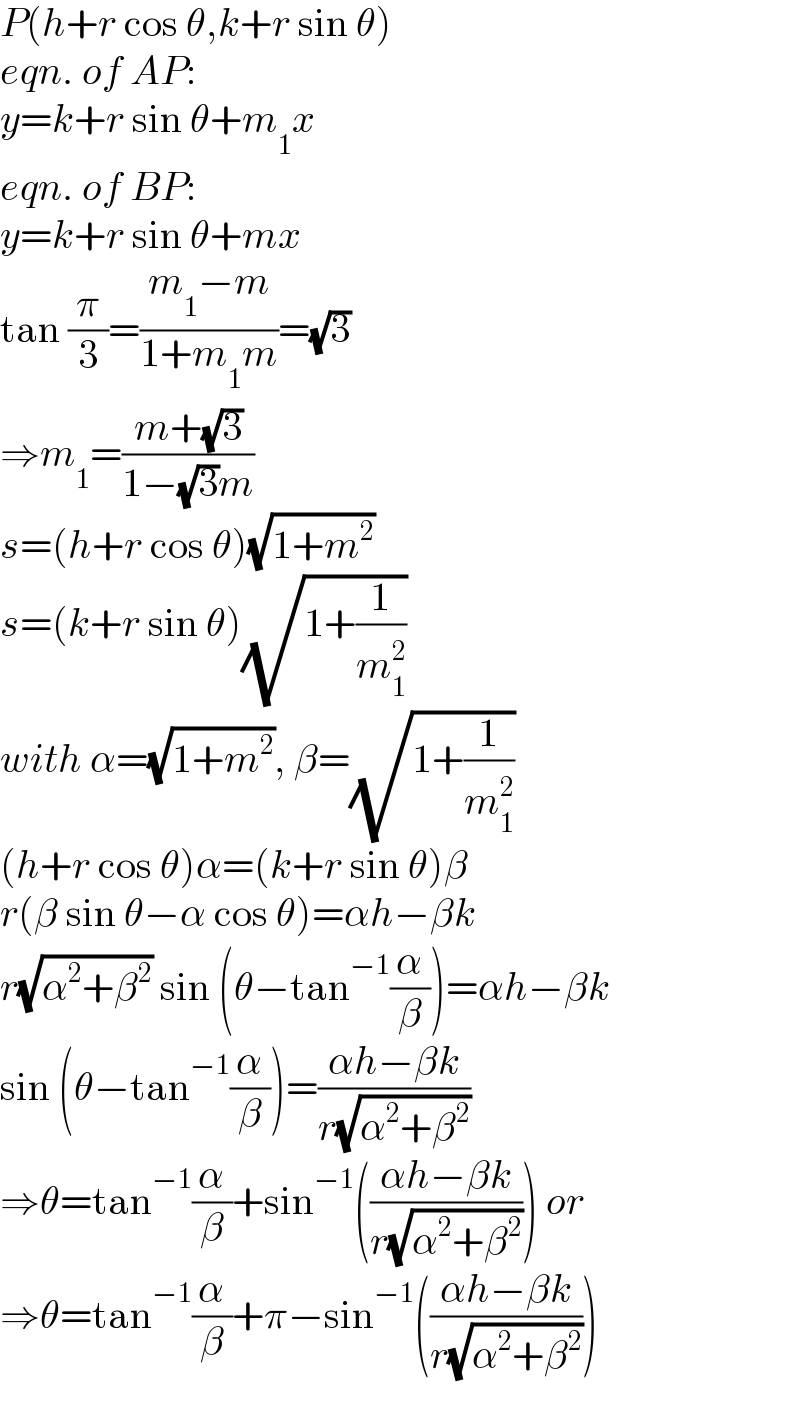
P(h+r cos θ,k+r sin θ) eqn. of AP: y=k+r sin θ+m_1 x eqn. of BP: y=k+r sin θ+mx tan (π/3)=((m_1 −m)/(1+m_1 m))=(√3) ⇒m_1 =((m+(√3))/(1−(√3)m)) s=(h+r cos θ)(√(1+m^2 )) s=(k+r sin θ)(√(1+(1/m_1 ^2 ))) with α=(√(1+m^2 )), β=(√(1+(1/m_1 ^2 ))) (h+r cos θ)α=(k+r sin θ)β r(β sin θ−α cos θ)=αh−βk r(√(α^2 +β^2 )) sin (θ−tan^(−1) (α/β))=αh−βk sin (θ−tan^(−1) (α/β))=((αh−βk)/(r(√(α^2 +β^2 )))) ⇒θ=tan^(−1) (α/β)+sin^(−1) (((αh−βk)/(r(√(α^2 +β^2 ))))) or ⇒θ=tan^(−1) (α/β)+π−sin^(−1) (((αh−βk)/(r(√(α^2 +β^2 )))))

$${P}\left({h}+{r}\:\mathrm{cos}\:\theta,{k}+{r}\:\mathrm{sin}\:\theta\right) \\ $$$${eqn}.\:{of}\:{AP}: \\ $$$${y}={k}+{r}\:\mathrm{sin}\:\theta+{m}_{\mathrm{1}} {x} \\ $$$${eqn}.\:{of}\:{BP}: \\ $$$${y}={k}+{r}\:\mathrm{sin}\:\theta+{mx} \\ $$$$\mathrm{tan}\:\frac{\pi}{\mathrm{3}}=\frac{{m}_{\mathrm{1}} −{m}}{\mathrm{1}+{m}_{\mathrm{1}} {m}}=\sqrt{\mathrm{3}} \\ $$$$\Rightarrow{m}_{\mathrm{1}} =\frac{{m}+\sqrt{\mathrm{3}}}{\mathrm{1}−\sqrt{\mathrm{3}}{m}} \\ $$$${s}=\left({h}+{r}\:\mathrm{cos}\:\theta\right)\sqrt{\mathrm{1}+{m}^{\mathrm{2}} } \\ $$$${s}=\left({k}+{r}\:\mathrm{sin}\:\theta\right)\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{m}_{\mathrm{1}} ^{\mathrm{2}} }} \\ $$$${with}\:\alpha=\sqrt{\mathrm{1}+{m}^{\mathrm{2}} },\:\beta=\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{m}_{\mathrm{1}} ^{\mathrm{2}} }} \\ $$$$\left({h}+{r}\:\mathrm{cos}\:\theta\right)\alpha=\left({k}+{r}\:\mathrm{sin}\:\theta\right)\beta \\ $$$${r}\left(\beta\:\mathrm{sin}\:\theta−\alpha\:\mathrm{cos}\:\theta\right)=\alpha{h}−\beta{k} \\ $$$${r}\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }\:\mathrm{sin}\:\left(\theta−\mathrm{tan}^{−\mathrm{1}} \frac{\alpha}{\beta}\right)=\alpha{h}−\beta{k} \\ $$$$\mathrm{sin}\:\left(\theta−\mathrm{tan}^{−\mathrm{1}} \frac{\alpha}{\beta}\right)=\frac{\alpha{h}−\beta{k}}{{r}\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }} \\ $$$$\Rightarrow\theta=\mathrm{tan}^{−\mathrm{1}} \frac{\alpha}{\beta}+\mathrm{sin}^{−\mathrm{1}} \left(\frac{\alpha{h}−\beta{k}}{{r}\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }}\right)\:{or} \\ $$$$\Rightarrow\theta=\mathrm{tan}^{−\mathrm{1}} \frac{\alpha}{\beta}+\pi−\mathrm{sin}^{−\mathrm{1}} \left(\frac{\alpha{h}−\beta{k}}{{r}\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }}\right) \\ $$

Commented by ajfour last updated on 08/Aug/21

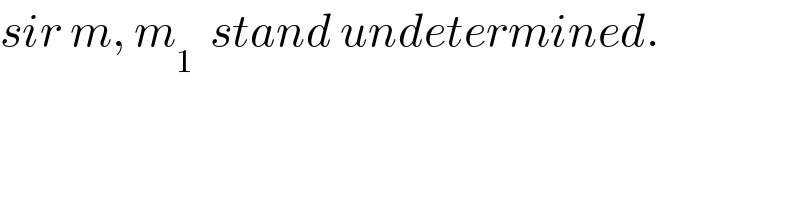
$${sir}\:{m},\:{m}_{\mathrm{1}} \:\:{stand}\:{undetermined}. \\ $$

Commented by mr W last updated on 08/Aug/21

i tried to find the length s in terms of m in following way: m_1 =((m+(√3))/(1−(√3)m)) α=(√(1+m^2 )), β=(√(1+(1/m_1 ^2 ))) θ=tan^(−1) (α/β)+sin^(−1) (((αh−βk)/(r(√(α^2 +β^2 ))))) or θ=tan^(−1) (α/β)+π−sin^(−1) (((αh−βk)/(r(√(α^2 +β^2 ))))) s=(h+r cos θ)(√(1+m^2 )) then graphically find the maximum and minimum of s.

$${i}\:{tried}\:{to}\:{find}\:{the}\:{length}\:{s}\:{in}\:{terms}\:{of} \\ $$$${m}\:{in}\:{following}\:{way}: \\ $$$${m}_{\mathrm{1}} =\frac{{m}+\sqrt{\mathrm{3}}}{\mathrm{1}−\sqrt{\mathrm{3}}{m}} \\ $$$$\alpha=\sqrt{\mathrm{1}+{m}^{\mathrm{2}} },\:\beta=\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{m}_{\mathrm{1}} ^{\mathrm{2}} }} \\ $$$$\theta=\mathrm{tan}^{−\mathrm{1}} \frac{\alpha}{\beta}+\mathrm{sin}^{−\mathrm{1}} \left(\frac{\alpha{h}−\beta{k}}{{r}\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }}\right)\:{or} \\ $$$$\theta=\mathrm{tan}^{−\mathrm{1}} \frac{\alpha}{\beta}+\pi−\mathrm{sin}^{−\mathrm{1}} \left(\frac{\alpha{h}−\beta{k}}{{r}\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }}\right) \\ $$$${s}=\left({h}+{r}\:\mathrm{cos}\:\theta\right)\sqrt{\mathrm{1}+{m}^{\mathrm{2}} } \\ $$$${then}\:{graphically}\:{find}\:{the}\:{maximum} \\ $$$${and}\:{minimum}\:{of}\:{s}. \\ $$

Commented by mr W last updated on 08/Aug/21

Facebook Tweet Pin

Leave a Reply Cancel reply