Question Number 150062 by 0731619 last updated on 09/Aug/21

Answered by Ar Brandon last updated on 09/Aug/21

$${li}_{\mathrm{2}} \left({x}\right)\underset{{function}} {\overset{{dilogarithm}} {=}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}^{\mathrm{2}} }=−\int_{\mathrm{0}} ^{\:{x}} \frac{{ln}\left(\mathrm{1}−{t}\right)}{{t}}{dt} \\ $$$$\Omega=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{Li}_{\mathrm{2}} \left({x}\right){dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}^{\mathrm{2}} }{dx} \\ $$$$\:\:\:\:=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}^{\mathrm{2}} }−\frac{\mathrm{1}}{{n}}+\frac{\mathrm{1}}{{n}+\mathrm{1}}\right) \\ $$$$\:\:\:\:=\zeta\left(\mathrm{2}\right)−{H}_{{n}} +{H}_{{n}} −\mathrm{1}=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\mathrm{1} \\ $$
Answered by mindispower last updated on 09/Aug/21
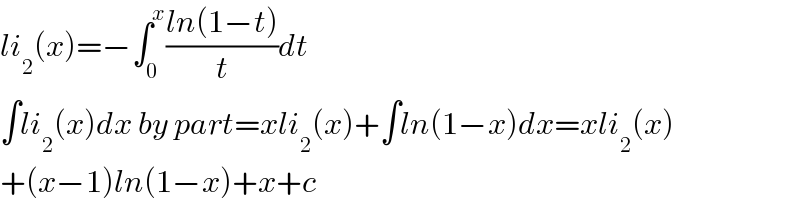
$${li}_{\mathrm{2}} \left({x}\right)=−\int_{\mathrm{0}} ^{{x}} \frac{{ln}\left(\mathrm{1}−{t}\right)}{{t}}{dt} \\ $$$$\int{li}_{\mathrm{2}} \left({x}\right){dx}\:{by}\:{part}={xli}_{\mathrm{2}} \left({x}\right)+\int{ln}\left(\mathrm{1}−{x}\right){dx}={xli}_{\mathrm{2}} \left({x}\right) \\ $$$$+\left({x}−\mathrm{1}\right){ln}\left(\mathrm{1}−{x}\right)+{x}+{c} \\ $$
