Question Number 150097 by mathdanisur last updated on 09/Aug/21
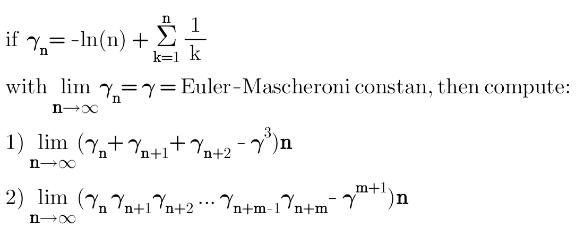
Answered by Kamel last updated on 09/Aug/21
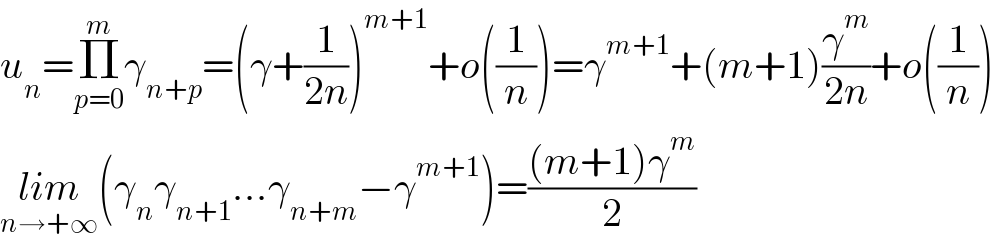
$${u}_{{n}} =\underset{{p}=\mathrm{0}} {\overset{{m}} {\prod}}\gamma_{{n}+{p}} =\left(\gamma+\frac{\mathrm{1}}{\mathrm{2}{n}}\right)^{{m}+\mathrm{1}} +{o}\left(\frac{\mathrm{1}}{{n}}\right)=\gamma^{{m}+\mathrm{1}} +\left({m}+\mathrm{1}\right)\frac{\gamma^{{m}} }{\mathrm{2}{n}}+{o}\left(\frac{\mathrm{1}}{{n}}\right) \\ $$$$\underset{{n}\rightarrow+\infty} {{lim}}\left(\gamma_{{n}} \gamma_{{n}+\mathrm{1}} …\gamma_{{n}+{m}} −\gamma^{{m}+\mathrm{1}} \right)=\frac{\left({m}+\mathrm{1}\right)\gamma^{{m}} }{\mathrm{2}} \\ $$
