Menu Close

Question-150177

Tinku Tara 0 Comments
Pin




Question Number 150177 by mr W last updated on 10/Aug/21
Commented by mr W last updated on 10/Aug/21
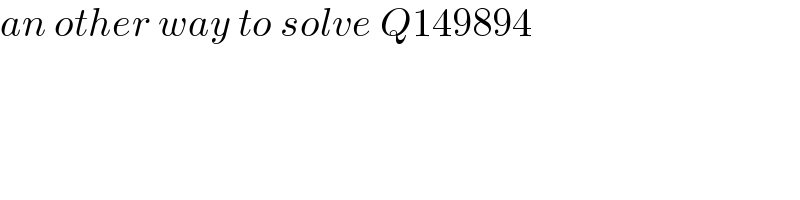
an other way to solve Q149894
$${an}\:{other}\:{way}\:{to}\:{solve}\:{Q}\mathrm{149894} \\ $$
Commented by mr W last updated on 10/Aug/21
the locus of the upper right vertex of the equilateral of side length s is an ellipse with major axis at 45° with a=((((√3)+1)s)/2), b=((((√3)−1)s)/2). therefore the question now is to find the two ellipses which tangent the circle.
$${the}\:{locus}\:{of}\:{the}\:{upper}\:{right}\:{vertex} \\ $$$${of}\:{the}\:{equilateral}\:{of}\:{side}\:{length}\:{s} \\ $$$${is}\:{an}\:{ellipse}\:{with}\:{major}\:{axis}\:{at}\:\mathrm{45}° \\ $$$${with}\:{a}=\frac{\left(\sqrt{\mathrm{3}}+\mathrm{1}\right){s}}{\mathrm{2}},\:{b}=\frac{\left(\sqrt{\mathrm{3}}−\mathrm{1}\right){s}}{\mathrm{2}}. \\ $$$${therefore}\:{the}\:{question}\:{now}\:\:{is}\:\:{to}\:{find} \\ $$$${the}\:{two}\:{ellipses}\:{which}\:{tangent}\:{the} \\ $$$${circle}. \\ $$
Commented by mr W last updated on 10/Aug/21
Commented by mr W last updated on 11/Aug/21
s=side length of equilateral a=(((√3)+1)/2)s=αs b=(((√3)−1)/2)s=βs (x^2 /α^2 )+(y^2 /β^2 )=s^2 (x−p)^2 +(y−q)^2 =r^2 say P(αs cos θ,βs sin θ) tan ϕ=(β/( α tan θ)) for s_(min) : x_C =αs cos θ+r sin ϕ x_C =αs cos θ+r (β/( (√(β^2 +α^2 tan^2 θ))))=p ⇒s_(min) =(1/(α cos θ))(p−r (β/( (√(β^2 +α^2 tan^2 θ))))) y_C =βs sin θ+r cos ϕ y_C =βs sin θ+r ((αtan θ)/( (√(β^2 +α^2 tan^2 θ))))=q ⇒s_(min) =(1/(β sin θ))(q−r ((αtan θ)/( (√(β^2 +α^2 tan^2 θ))))) (1/(α cos θ))(p−r (β/( (√(β^2 +α^2 tan^2 θ)))))=(1/(β sin θ))(q−r ((αtan θ)/( (√(β^2 +α^2 tan^2 θ))))) ⇒((αq)/(tan θ))−(((α^2 −β^2 )r)/( (√(β^2 +α^2 tan^2 θ))))=βp similarly for s_(max) : s_(max) =(1/(α cos θ))(p+r (β/( (√(β^2 +α^2 tan^2 θ))))) s_(max) =(1/(β sin θ))(q+r ((αtan θ)/( (√(β^2 +α^2 tan^2 θ))))) ((αq)/(tan θ))+(((α^2 −β^2 )r)/( (√(β^2 +α^2 tan^2 θ))))=βp with p=((k+h)/( (√2))), q=((k−h)/( (√2))) example: h=6, k=8, r=2 p=7(√2), q=(√2) s_(max) =11.9086 ✓ s_(min) =6.0829 ✓
$${s}={side}\:{length}\:{of}\:{equilateral} \\ $$$${a}=\frac{\sqrt{\mathrm{3}}+\mathrm{1}}{\mathrm{2}}{s}=\alpha{s} \\ $$$${b}=\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{2}}{s}=\beta{s} \\ $$$$\frac{{x}^{\mathrm{2}} }{\alpha^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{\beta^{\mathrm{2}} }={s}^{\mathrm{2}} \\ $$$$\left({x}−{p}\right)^{\mathrm{2}} +\left({y}−{q}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$${say}\:{P}\left(\alpha{s}\:\mathrm{cos}\:\theta,\beta{s}\:\mathrm{sin}\:\theta\right) \\ $$$$\mathrm{tan}\:\varphi=\frac{\beta}{\:\alpha\:\mathrm{tan}\:\theta} \\ $$$${for}\:{s}_{{min}} : \\ $$$${x}_{{C}} =\alpha{s}\:\mathrm{cos}\:\theta+{r}\:\mathrm{sin}\:\varphi \\ $$$${x}_{{C}} =\alpha{s}\:\mathrm{cos}\:\theta+{r}\:\frac{\beta}{\:\sqrt{\beta^{\mathrm{2}} +\alpha^{\mathrm{2}} \mathrm{tan}^{\mathrm{2}} \:\theta}}={p} \\ $$$$\Rightarrow{s}_{{min}} =\frac{\mathrm{1}}{\alpha\:\mathrm{cos}\:\theta}\left({p}−{r}\:\frac{\beta}{\:\sqrt{\beta^{\mathrm{2}} +\alpha^{\mathrm{2}} \mathrm{tan}^{\mathrm{2}} \:\theta}}\right) \\ $$$${y}_{{C}} =\beta{s}\:\mathrm{sin}\:\theta+{r}\:\mathrm{cos}\:\varphi \\ $$$${y}_{{C}} =\beta{s}\:\mathrm{sin}\:\theta+{r}\:\frac{\alpha\mathrm{tan}\:\theta}{\:\sqrt{\beta^{\mathrm{2}} +\alpha^{\mathrm{2}} \mathrm{tan}^{\mathrm{2}} \:\theta}}={q} \\ $$$$\Rightarrow{s}_{{min}} =\frac{\mathrm{1}}{\beta\:\mathrm{sin}\:\theta}\left({q}−{r}\:\frac{\alpha\mathrm{tan}\:\theta}{\:\sqrt{\beta^{\mathrm{2}} +\alpha^{\mathrm{2}} \mathrm{tan}^{\mathrm{2}} \:\theta}}\right) \\ $$$$\frac{\mathrm{1}}{\alpha\:\mathrm{cos}\:\theta}\left({p}−{r}\:\frac{\beta}{\:\sqrt{\beta^{\mathrm{2}} +\alpha^{\mathrm{2}} \mathrm{tan}^{\mathrm{2}} \:\theta}}\right)=\frac{\mathrm{1}}{\beta\:\mathrm{sin}\:\theta}\left({q}−{r}\:\frac{\alpha\mathrm{tan}\:\theta}{\:\sqrt{\beta^{\mathrm{2}} +\alpha^{\mathrm{2}} \mathrm{tan}^{\mathrm{2}} \:\theta}}\right) \\ $$$$\Rightarrow\frac{\alpha{q}}{\mathrm{tan}\:\theta}−\frac{\left(\alpha^{\mathrm{2}} −\beta^{\mathrm{2}} \right){r}}{\:\sqrt{\beta^{\mathrm{2}} +\alpha^{\mathrm{2}} \mathrm{tan}^{\mathrm{2}} \:\theta}}=\beta{p} \\ $$$$ \\ $$$${similarly}\:{for}\:{s}_{{max}} : \\ $$$${s}_{{max}} =\frac{\mathrm{1}}{\alpha\:\mathrm{cos}\:\theta}\left({p}+{r}\:\frac{\beta}{\:\sqrt{\beta^{\mathrm{2}} +\alpha^{\mathrm{2}} \mathrm{tan}^{\mathrm{2}} \:\theta}}\right) \\ $$$${s}_{{max}} =\frac{\mathrm{1}}{\beta\:\mathrm{sin}\:\theta}\left({q}+{r}\:\frac{\alpha\mathrm{tan}\:\theta}{\:\sqrt{\beta^{\mathrm{2}} +\alpha^{\mathrm{2}} \mathrm{tan}^{\mathrm{2}} \:\theta}}\right) \\ $$$$\frac{\alpha{q}}{\mathrm{tan}\:\theta}+\frac{\left(\alpha^{\mathrm{2}} −\beta^{\mathrm{2}} \right){r}}{\:\sqrt{\beta^{\mathrm{2}} +\alpha^{\mathrm{2}} \mathrm{tan}^{\mathrm{2}} \:\theta}}=\beta{p} \\ $$$$ \\ $$$${with}\:{p}=\frac{{k}+{h}}{\:\sqrt{\mathrm{2}}},\:{q}=\frac{{k}−{h}}{\:\sqrt{\mathrm{2}}} \\ $$$$ \\ $$$${example}:\:{h}=\mathrm{6},\:{k}=\mathrm{8},\:{r}=\mathrm{2} \\ $$$${p}=\mathrm{7}\sqrt{\mathrm{2}},\:{q}=\sqrt{\mathrm{2}} \\ $$$${s}_{{max}} =\mathrm{11}.\mathrm{9086}\:\checkmark \\ $$$${s}_{{min}} =\mathrm{6}.\mathrm{0829}\:\checkmark \\ $$
Commented by mr W last updated on 12/Aug/21
summary: α=(((√3)+1)/2), β=(((√3)−1)/2) p=((k+h)/( (√2))), q=((k−h)/( (√2))) s_(max/min) =(1/α)((p/(cos θ))±((βr)/( (√(α^2 sin^2 θ+β^2 cos^2 θ))))) with θ from ((αq)/(tan θ))±(((α^2 −β^2 )r)/( (√(β^2 +α^2 tan^2 θ))))=βp (+ for s_(max) and − for s_(min) )
$${summary}: \\ $$$$\alpha=\frac{\sqrt{\mathrm{3}}+\mathrm{1}}{\mathrm{2}},\:\beta=\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{2}} \\ $$$${p}=\frac{{k}+{h}}{\:\sqrt{\mathrm{2}}},\:{q}=\frac{{k}−{h}}{\:\sqrt{\mathrm{2}}} \\ $$$${s}_{{max}/{min}} =\frac{\mathrm{1}}{\alpha}\left(\frac{{p}}{\mathrm{cos}\:\theta}\pm\frac{\beta{r}}{\:\sqrt{\alpha^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta+\beta^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta}}\right) \\ $$$${with}\:\theta\:{from} \\ $$$$\frac{\alpha{q}}{\mathrm{tan}\:\theta}\pm\frac{\left(\alpha^{\mathrm{2}} −\beta^{\mathrm{2}} \right){r}}{\:\sqrt{\beta^{\mathrm{2}} +\alpha^{\mathrm{2}} \mathrm{tan}^{\mathrm{2}} \:\theta}}=\beta{p} \\ $$$$ \\ $$$$\left(+\:{for}\:{s}_{{max}} \:{and}\:−\:{for}\:{s}_{{min}} \right) \\ $$
Answered by mr W last updated on 10/Aug/21
Commented by mr W last updated on 10/Aug/21
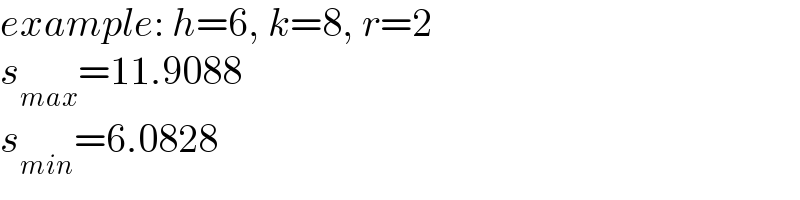
example: h=6, k=8, r=2 s_(max) =11.9088 s_(min) =6.0828
$${example}:\:{h}=\mathrm{6},\:{k}=\mathrm{8},\:{r}=\mathrm{2} \\ $$$${s}_{{max}} =\mathrm{11}.\mathrm{9088} \\ $$$${s}_{{min}} =\mathrm{6}.\mathrm{0828} \\ $$
Commented by mr W last updated on 10/Aug/21
Commented by mr W last updated on 10/Aug/21
C(h,k) D((s/2)cos φ, (s/2)sin φ) x_P =(s/2)cos φ+(((√3)s)/2)sin φ=s sin (φ+(π/6)) y_P =(s/2)sin φ+(((√3)s)/2)cos φ=s sin (φ+(π/3)) [s sin (φ+(π/6))−h]^2 +[s sin (φ+(π/3))−k]^2 =r^2 [sin^2 (φ+(π/6))+sin^2 (φ+(π/3))]s^2 −2[h sin (φ+(π/6))+k sin (φ+(π/3))]s+(h^2 +k^2 −r^2 )=0 u(φ)s^2 −2v(φ)s+(h^2 +k^2 −r^2 )=0 s=((v(φ)±(√(v^2 (φ)−(h^2 +k^2 −r^2 )u(φ))))/(u(φ))) with u(φ)=sin^2 (φ+(π/6))+sin^2 (φ+(π/3)) v(φ)=h sin (φ+(π/6))+k sin (φ+(π/3))
$${C}\left({h},{k}\right) \\ $$$${D}\left(\frac{{s}}{\mathrm{2}}\mathrm{cos}\:\phi,\:\frac{{s}}{\mathrm{2}}\mathrm{sin}\:\phi\right) \\ $$$${x}_{{P}} =\frac{{s}}{\mathrm{2}}\mathrm{cos}\:\phi+\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{2}}\mathrm{sin}\:\phi={s}\:\mathrm{sin}\:\left(\phi+\frac{\pi}{\mathrm{6}}\right) \\ $$$${y}_{{P}} =\frac{{s}}{\mathrm{2}}\mathrm{sin}\:\phi+\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{2}}\mathrm{cos}\:\phi={s}\:\mathrm{sin}\:\left(\phi+\frac{\pi}{\mathrm{3}}\right) \\ $$$$\left[{s}\:\mathrm{sin}\:\left(\phi+\frac{\pi}{\mathrm{6}}\right)−{h}\right]^{\mathrm{2}} +\left[{s}\:\mathrm{sin}\:\left(\phi+\frac{\pi}{\mathrm{3}}\right)−{k}\right]^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\left[\mathrm{sin}^{\mathrm{2}} \:\left(\phi+\frac{\pi}{\mathrm{6}}\right)+\mathrm{sin}^{\mathrm{2}} \:\left(\phi+\frac{\pi}{\mathrm{3}}\right)\right]{s}^{\mathrm{2}} −\mathrm{2}\left[{h}\:\mathrm{sin}\:\left(\phi+\frac{\pi}{\mathrm{6}}\right)+{k}\:\mathrm{sin}\:\left(\phi+\frac{\pi}{\mathrm{3}}\right)\right]{s}+\left({h}^{\mathrm{2}} +{k}^{\mathrm{2}} −{r}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$${u}\left(\phi\right){s}^{\mathrm{2}} −\mathrm{2}{v}\left(\phi\right){s}+\left({h}^{\mathrm{2}} +{k}^{\mathrm{2}} −{r}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$${s}=\frac{{v}\left(\phi\right)\pm\sqrt{{v}^{\mathrm{2}} \left(\phi\right)−\left({h}^{\mathrm{2}} +{k}^{\mathrm{2}} −{r}^{\mathrm{2}} \right){u}\left(\phi\right)}}{{u}\left(\phi\right)} \\ $$$${with}\: \\ $$$${u}\left(\phi\right)=\mathrm{sin}^{\mathrm{2}} \:\left(\phi+\frac{\pi}{\mathrm{6}}\right)+\mathrm{sin}^{\mathrm{2}} \:\left(\phi+\frac{\pi}{\mathrm{3}}\right) \\ $$$${v}\left(\phi\right)={h}\:\mathrm{sin}\:\left(\phi+\frac{\pi}{\mathrm{6}}\right)+{k}\:\mathrm{sin}\:\left(\phi+\frac{\pi}{\mathrm{3}}\right) \\ $$
Commented by mr W last updated on 10/Aug/21
Commented by mr W last updated on 10/Aug/21

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *