Question Number 150351 by eman_64 last updated on 11/Aug/21
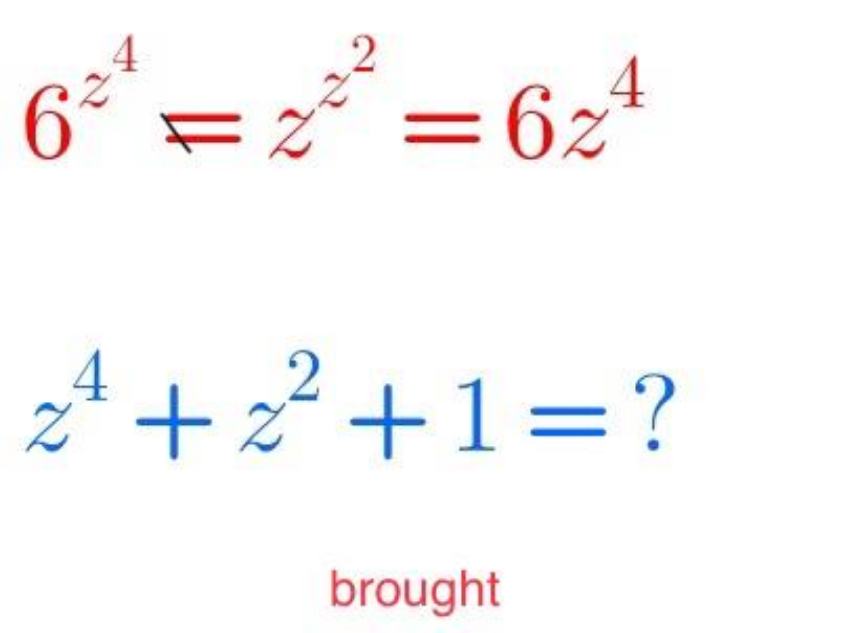
Commented by eman_64 last updated on 11/Aug/21

$$\:\mathrm{How}\:\mathrm{do} \\ $$
Commented by mathdanisur last updated on 11/Aug/21

$$=\mathrm{5}\sqrt{\mathrm{3}}+\mathrm{10} \\ $$
Answered by aleks041103 last updated on 12/Aug/21
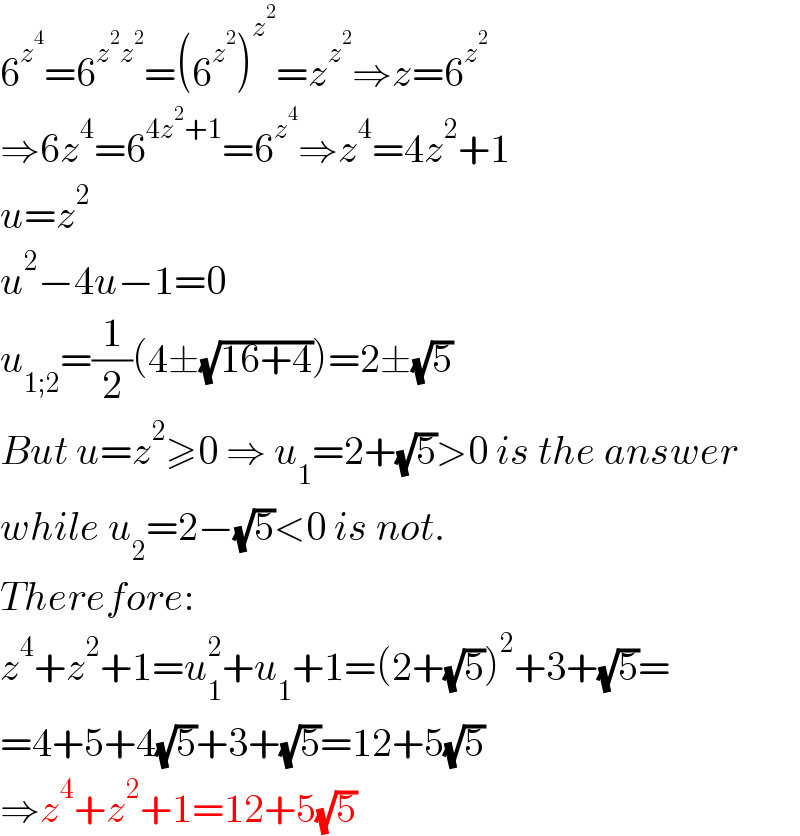
$$\mathrm{6}^{{z}^{\mathrm{4}} } =\mathrm{6}^{{z}^{\mathrm{2}} {z}^{\mathrm{2}} } =\left(\mathrm{6}^{{z}^{\mathrm{2}} } \right)^{{z}^{\mathrm{2}} } ={z}^{{z}^{\mathrm{2}} } \Rightarrow{z}=\mathrm{6}^{{z}^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{6}{z}^{\mathrm{4}} =\mathrm{6}^{\mathrm{4}{z}^{\mathrm{2}} +\mathrm{1}} =\mathrm{6}^{{z}^{\mathrm{4}} } \Rightarrow{z}^{\mathrm{4}} =\mathrm{4}{z}^{\mathrm{2}} +\mathrm{1} \\ $$$${u}={z}^{\mathrm{2}} \\ $$$${u}^{\mathrm{2}} −\mathrm{4}{u}−\mathrm{1}=\mathrm{0} \\ $$$${u}_{\mathrm{1};\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{4}\pm\sqrt{\mathrm{16}+\mathrm{4}}\right)=\mathrm{2}\pm\sqrt{\mathrm{5}} \\ $$$${But}\:{u}={z}^{\mathrm{2}} \geqslant\mathrm{0}\:\Rightarrow\:{u}_{\mathrm{1}} =\mathrm{2}+\sqrt{\mathrm{5}}>\mathrm{0}\:{is}\:{the}\:{answer} \\ $$$${while}\:{u}_{\mathrm{2}} =\mathrm{2}−\sqrt{\mathrm{5}}<\mathrm{0}\:{is}\:{not}. \\ $$$${Therefore}: \\ $$$${z}^{\mathrm{4}} +{z}^{\mathrm{2}} +\mathrm{1}={u}_{\mathrm{1}} ^{\mathrm{2}} +{u}_{\mathrm{1}} +\mathrm{1}=\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)^{\mathrm{2}} +\mathrm{3}+\sqrt{\mathrm{5}}= \\ $$$$=\mathrm{4}+\mathrm{5}+\mathrm{4}\sqrt{\mathrm{5}}+\mathrm{3}+\sqrt{\mathrm{5}}=\mathrm{12}+\mathrm{5}\sqrt{\mathrm{5}} \\ $$$$\Rightarrow{z}^{\mathrm{4}} +{z}^{\mathrm{2}} +\mathrm{1}=\mathrm{12}+\mathrm{5}\sqrt{\mathrm{5}} \\ $$
