Question Number 150372 by tabata last updated on 11/Aug/21

Commented by mathdanisur last updated on 11/Aug/21
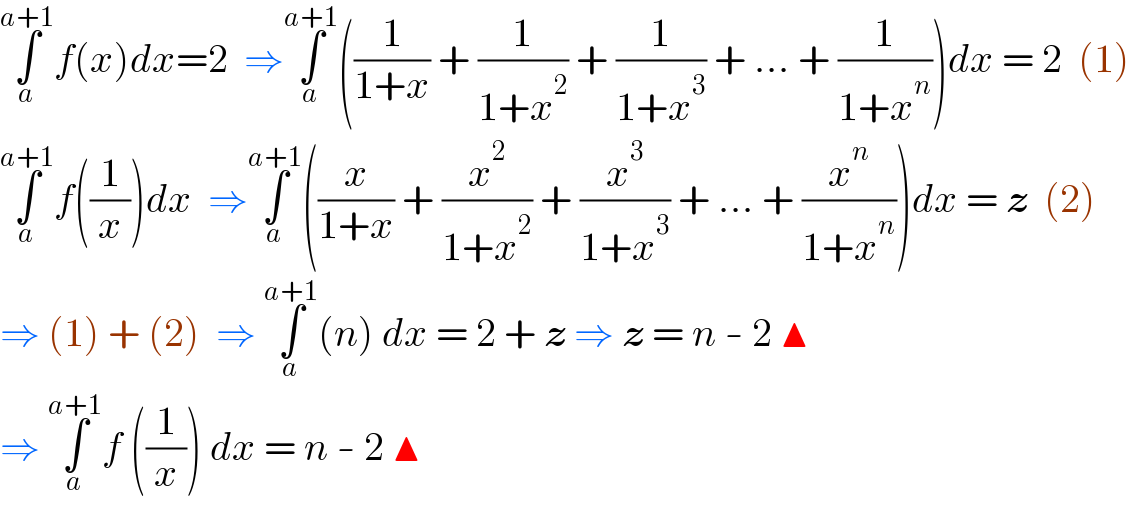
$$\underset{{a}} {\overset{{a}+\mathrm{1}} {\int}}{f}\left({x}\right){dx}=\mathrm{2}\:\:\Rightarrow\underset{{a}} {\overset{{a}+\mathrm{1}} {\int}}\left(\frac{\mathrm{1}}{\mathrm{1}+{x}}\:+\:\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{3}} }\:+\:…\:+\:\frac{\mathrm{1}}{\mathrm{1}+{x}^{{n}} }\right){dx}\:=\:\mathrm{2}\:\:\left(\mathrm{1}\right) \\ $$$$\underset{{a}} {\overset{{a}+\mathrm{1}} {\int}}{f}\left(\frac{\mathrm{1}}{{x}}\right){dx}\:\:\Rightarrow\underset{{a}} {\overset{{a}+\mathrm{1}} {\int}}\left(\frac{{x}}{\mathrm{1}+{x}}\:+\:\frac{{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }\:+\:\frac{{x}^{\mathrm{3}} }{\mathrm{1}+{x}^{\mathrm{3}} }\:+\:…\:+\:\frac{{x}^{{n}} }{\mathrm{1}+{x}^{{n}} }\right){dx}\:=\:\boldsymbol{{z}}\:\:\left(\mathrm{2}\right) \\ $$$$\Rightarrow\:\left(\mathrm{1}\right)\:+\:\left(\mathrm{2}\right)\:\:\Rightarrow\:\underset{{a}} {\overset{{a}+\mathrm{1}} {\int}}\left({n}\right)\:{dx}\:=\:\mathrm{2}\:+\:\boldsymbol{{z}}\:\Rightarrow\:\boldsymbol{{z}}\:=\:{n}\:-\:\mathrm{2}\:\blacktriangle \\ $$$$\Rightarrow\:\underset{{a}} {\overset{{a}+\mathrm{1}} {\int}}{f}\:\left(\frac{\mathrm{1}}{{x}}\right)\:{dx}\:=\:{n}\:-\:\mathrm{2}\:\blacktriangle \\ $$
