Question-150376

Question Number 150376 by cherokeesay last updated on 11/Aug/21

Commented by liberty last updated on 12/Aug/21

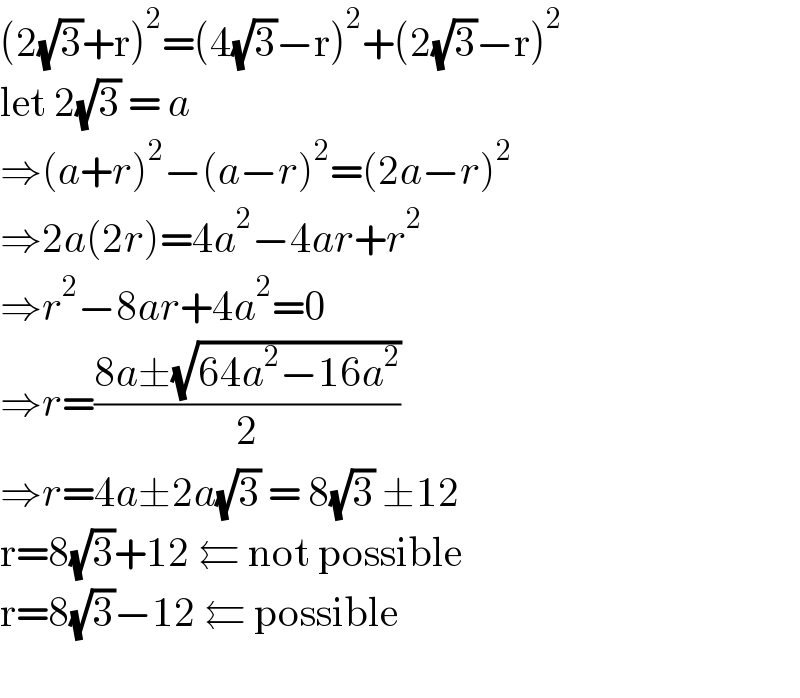
(2(√3)+r)^2 =(4(√3)−r)^2 +(2(√3)−r)^2 let 2(√3) = a ⇒(a+r)^2 −(a−r)^2 =(2a−r)^2 ⇒2a(2r)=4a^2 −4ar+r^2 ⇒r^2 −8ar+4a^2 =0 ⇒r=((8a±(√(64a^2 −16a^2 )))/2) ⇒r=4a±2a(√3) = 8(√3) ±12 r=8(√3)+12 ⇇ not possible r=8(√3)−12 ⇇ possible

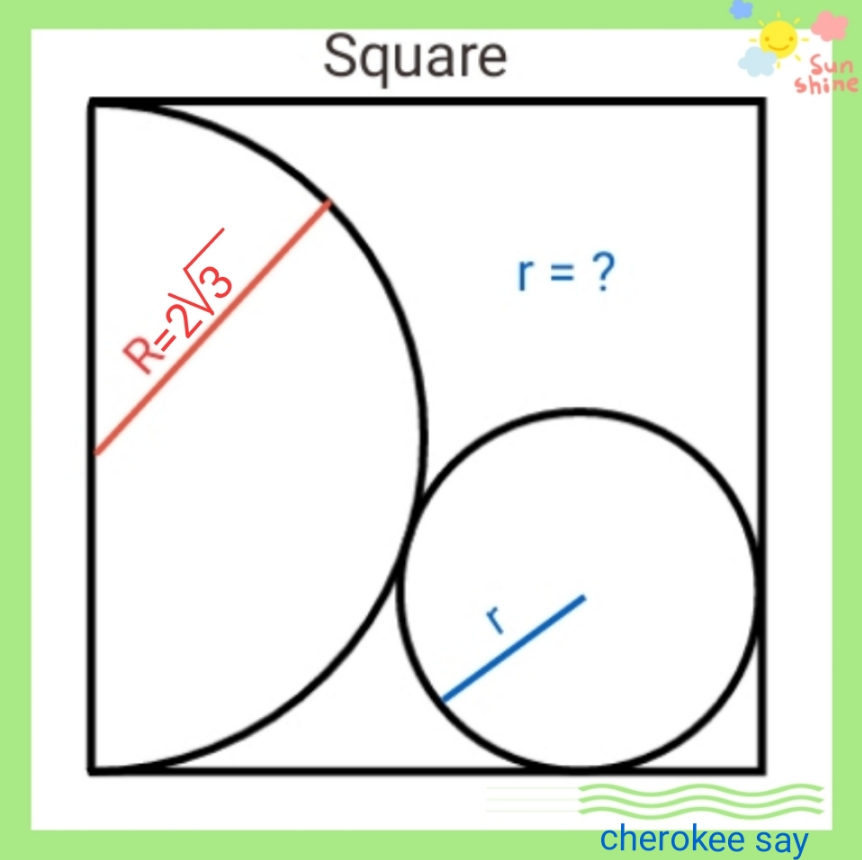
$$\left(\mathrm{2}\sqrt{\mathrm{3}}+\mathrm{r}\right)^{\mathrm{2}} =\left(\mathrm{4}\sqrt{\mathrm{3}}−\mathrm{r}\right)^{\mathrm{2}} +\left(\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{r}\right)^{\mathrm{2}} \\ $$$$\mathrm{let}\:\mathrm{2}\sqrt{\mathrm{3}}\:=\:{a} \\ $$$$\Rightarrow\left({a}+{r}\right)^{\mathrm{2}} −\left({a}−{r}\right)^{\mathrm{2}} =\left(\mathrm{2}{a}−{r}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}{a}\left(\mathrm{2}{r}\right)=\mathrm{4}{a}^{\mathrm{2}} −\mathrm{4}{ar}+{r}^{\mathrm{2}} \\ $$$$\Rightarrow{r}^{\mathrm{2}} −\mathrm{8}{ar}+\mathrm{4}{a}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{r}=\frac{\mathrm{8}{a}\pm\sqrt{\mathrm{64}{a}^{\mathrm{2}} −\mathrm{16}{a}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$$\Rightarrow{r}=\mathrm{4}{a}\pm\mathrm{2}{a}\sqrt{\mathrm{3}}\:=\:\mathrm{8}\sqrt{\mathrm{3}}\:\pm\mathrm{12} \\ $$$$\mathrm{r}=\mathrm{8}\sqrt{\mathrm{3}}+\mathrm{12}\:\leftleftarrows\:\mathrm{not}\:\mathrm{possible} \\ $$$$\mathrm{r}=\mathrm{8}\sqrt{\mathrm{3}}−\mathrm{12}\:\leftleftarrows\:\mathrm{possible} \\ $$$$ \\ $$

Commented by cherokeesay last updated on 12/Aug/21