Question Number 150413 by saly last updated on 12/Aug/21
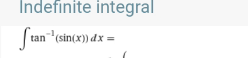
Commented by MJS_new last updated on 12/Aug/21
![in this case we must take the long way home... (1) arctan r =−(i/2)(ln (1+ir) −ln (1−ir)) ⇒ ∫arctan sin x dx= =−(i/2)(∫ln (1+i sin x) dx−∫ln (1−i sin x) dx) (2) sin α =((e^(iα) −e^(−iα) )/(2i)) ⇒ [similar for the 2^(nd) integral] ∫ln (1+i sin x) dx= =∫ln (1+(e^(ix) /2)−(1/(2e^(ix) ))) dx (3) t=ix ⇔ x=−it → dx=−idt ⇒ ∫ln (1+(e^(ix) /2)−(1/(2e^(ix) ))) dx= =iln 2∫dt −i∫ln (2+e^t −e^(−t) ) dt (4) by parts ⇒ ∫ln (2+e^t −e^(−t) ) dt= =tln (2+e^t −e^(−t) ) −∫((t(e^(2t) +1))/(e^(2t) −2e^t −1))dt (5) u=e^t ⇔ t=ln u → dt=(du/u) ⇒ ∫((t(e^(2t) +1))/(e^(2t) −2e^t −1))dt= =∫(((u^2 +1)ln u)/(u(u^2 −2u−1)))du= =2∫((uln u)/(u^2 −2u−1))du−2∫((ln u)/(u^2 −2u−1))du−∫((ln u)/u)du and I hope you can do these yourself](https://www.tinkutara.com/question/Q150417.png)
$$\mathrm{in}\:\mathrm{this}\:\mathrm{case}\:\mathrm{we}\:\mathrm{must}\:\mathrm{take}\:\mathrm{the}\:\mathrm{long}\:\mathrm{way}\:\mathrm{home}… \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\:\mathrm{arctan}\:{r}\:=−\frac{\mathrm{i}}{\mathrm{2}}\left(\mathrm{ln}\:\left(\mathrm{1}+\mathrm{i}{r}\right)\:−\mathrm{ln}\:\left(\mathrm{1}−\mathrm{i}{r}\right)\right) \\ $$$$\Rightarrow \\ $$$$\int\mathrm{arctan}\:\mathrm{sin}\:{x}\:{dx}= \\ $$$$=−\frac{\mathrm{i}}{\mathrm{2}}\left(\int\mathrm{ln}\:\left(\mathrm{1}+\mathrm{i}\:\mathrm{sin}\:{x}\right)\:{dx}−\int\mathrm{ln}\:\left(\mathrm{1}−\mathrm{i}\:\mathrm{sin}\:{x}\right)\:{dx}\right) \\ $$$$ \\ $$$$\left(\mathrm{2}\right)\:\mathrm{sin}\:\alpha\:=\frac{\mathrm{e}^{\mathrm{i}\alpha} −\mathrm{e}^{−\mathrm{i}\alpha} }{\mathrm{2i}} \\ $$$$\Rightarrow \\ $$$$\left[\mathrm{similar}\:\mathrm{for}\:\mathrm{the}\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{integral}\right] \\ $$$$\int\mathrm{ln}\:\left(\mathrm{1}+\mathrm{i}\:\mathrm{sin}\:{x}\right)\:{dx}= \\ $$$$=\int\mathrm{ln}\:\left(\mathrm{1}+\frac{\mathrm{e}^{\mathrm{i}{x}} }{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2e}^{\mathrm{i}{x}} }\right)\:{dx} \\ $$$$ \\ $$$$\left(\mathrm{3}\right)\:{t}=\mathrm{i}{x}\:\Leftrightarrow\:{x}=−\mathrm{i}{t}\:\rightarrow\:{dx}=−\mathrm{i}{dt} \\ $$$$\Rightarrow \\ $$$$\int\mathrm{ln}\:\left(\mathrm{1}+\frac{\mathrm{e}^{\mathrm{i}{x}} }{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2e}^{\mathrm{i}{x}} }\right)\:{dx}= \\ $$$$=\mathrm{iln}\:\mathrm{2}\int{dt}\:−\mathrm{i}\int\mathrm{ln}\:\left(\mathrm{2}+\mathrm{e}^{{t}} −\mathrm{e}^{−{t}} \right)\:{dt} \\ $$$$ \\ $$$$\left(\mathrm{4}\right)\:\mathrm{by}\:\mathrm{parts} \\ $$$$\Rightarrow \\ $$$$\int\mathrm{ln}\:\left(\mathrm{2}+\mathrm{e}^{{t}} −\mathrm{e}^{−{t}} \right)\:{dt}= \\ $$$$={t}\mathrm{ln}\:\left(\mathrm{2}+\mathrm{e}^{{t}} −\mathrm{e}^{−{t}} \right)\:−\int\frac{{t}\left(\mathrm{e}^{\mathrm{2}{t}} +\mathrm{1}\right)}{\mathrm{e}^{\mathrm{2}{t}} −\mathrm{2e}^{{t}} −\mathrm{1}}{dt} \\ $$$$ \\ $$$$\left(\mathrm{5}\right)\:{u}=\mathrm{e}^{{t}} \:\Leftrightarrow\:{t}=\mathrm{ln}\:{u}\:\rightarrow\:{dt}=\frac{{du}}{{u}} \\ $$$$\Rightarrow \\ $$$$\int\frac{{t}\left(\mathrm{e}^{\mathrm{2}{t}} +\mathrm{1}\right)}{\mathrm{e}^{\mathrm{2}{t}} −\mathrm{2e}^{{t}} −\mathrm{1}}{dt}= \\ $$$$=\int\frac{\left({u}^{\mathrm{2}} +\mathrm{1}\right)\mathrm{ln}\:{u}}{{u}\left({u}^{\mathrm{2}} −\mathrm{2}{u}−\mathrm{1}\right)}{du}= \\ $$$$=\mathrm{2}\int\frac{{u}\mathrm{ln}\:{u}}{{u}^{\mathrm{2}} −\mathrm{2}{u}−\mathrm{1}}{du}−\mathrm{2}\int\frac{\mathrm{ln}\:{u}}{{u}^{\mathrm{2}} −\mathrm{2}{u}−\mathrm{1}}{du}−\int\frac{\mathrm{ln}\:{u}}{{u}}{du} \\ $$$$ \\ $$$$\mathrm{and}\:\mathrm{I}\:\mathrm{hope}\:\mathrm{you}\:\mathrm{can}\:\mathrm{do}\:\mathrm{these}\:\mathrm{yourself} \\ $$
Commented by saly last updated on 12/Aug/21

$$\:\:{Thank}\:{sir} \\ $$
Commented by MJS_new last updated on 12/Aug/21

$$\mathrm{you}'\mathrm{re}\:\mathrm{welcome}. \\ $$
