Question Number 150508 by saly last updated on 13/Aug/21
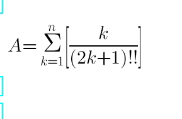
Commented by saly last updated on 13/Aug/21

$$\:{Do}\:{you}\:{help}\:{me}? \\ $$
Answered by Olaf_Thorendsen last updated on 13/Aug/21
![A = Σ_(k=1) ^n [(k/((2k+1)!!))] ∀k∈{1,...n}, (2k+1)!! > k ⇒ [(k/((2k+1)!!))] = 0 ⇒ A = 0 (if [x] means integer part of x)](https://www.tinkutara.com/question/Q150584.png)
$$\mathrm{A}\:=\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left[\frac{{k}}{\left(\mathrm{2}{k}+\mathrm{1}\right)!!}\right] \\ $$$$\forall{k}\in\left\{\mathrm{1},…{n}\right\},\:\left(\mathrm{2}{k}+\mathrm{1}\right)!!\:>\:{k} \\ $$$$\Rightarrow\:\left[\frac{{k}}{\left(\mathrm{2}{k}+\mathrm{1}\right)!!}\right]\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{A}\:=\:\mathrm{0} \\ $$$$\left(\mathrm{if}\:\left[{x}\right]\:\mathrm{means}\:\mathrm{integer}\:\mathrm{part}\:\mathrm{of}\:{x}\right) \\ $$
Commented by saly last updated on 14/Aug/21

$$\:\:{thank}\:{you}\: \\ $$
