Question Number 150515 by mathdanisur last updated on 13/Aug/21
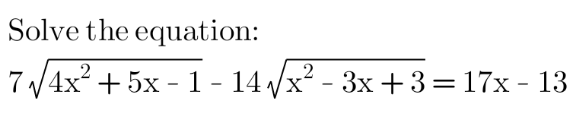
Answered by ajfour last updated on 13/Aug/21
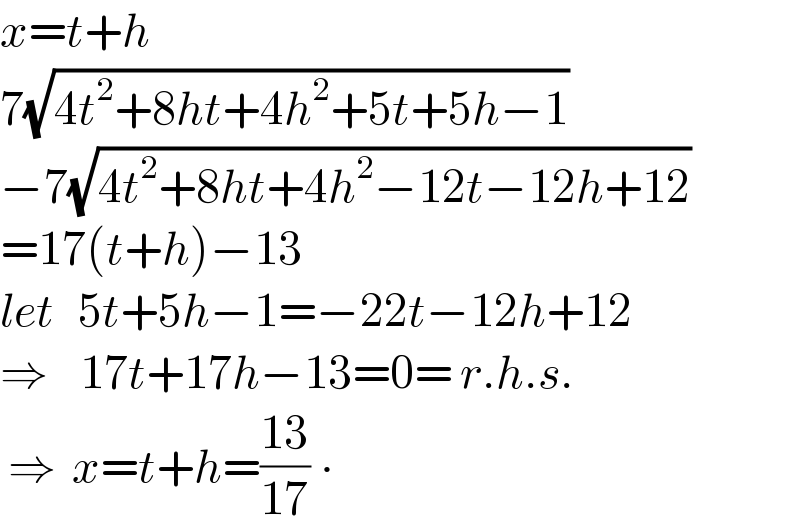
$${x}={t}+{h} \\ $$$$\mathrm{7}\sqrt{\mathrm{4}{t}^{\mathrm{2}} +\mathrm{8}{ht}+\mathrm{4}{h}^{\mathrm{2}} +\mathrm{5}{t}+\mathrm{5}{h}−\mathrm{1}} \\ $$$$−\mathrm{7}\sqrt{\mathrm{4}{t}^{\mathrm{2}} +\mathrm{8}{ht}+\mathrm{4}{h}^{\mathrm{2}} −\mathrm{12}{t}−\mathrm{12}{h}+\mathrm{12}} \\ $$$$=\mathrm{17}\left({t}+{h}\right)−\mathrm{13} \\ $$$${let}\:\:\:\mathrm{5}{t}+\mathrm{5}{h}−\mathrm{1}=−\mathrm{22}{t}−\mathrm{12}{h}+\mathrm{12} \\ $$$$\Rightarrow\:\:\:\:\mathrm{17}{t}+\mathrm{17}{h}−\mathrm{13}=\mathrm{0}=\:{r}.{h}.{s}. \\ $$$$\:\Rightarrow\:\:{x}={t}+{h}=\frac{\mathrm{13}}{\mathrm{17}}\:\centerdot \\ $$
Commented by MJS_new last updated on 13/Aug/21

$$\mathrm{yes}.\:\mathrm{but}\:\mathrm{there}\:\mathrm{are}\:\mathrm{3}\:\mathrm{solutions} \\ $$$${x}_{\mathrm{1}} =−\frac{\mathrm{746}}{\mathrm{495}} \\ $$$${x}_{\mathrm{2}} =\frac{\mathrm{13}}{\mathrm{17}} \\ $$$${x}_{\mathrm{3}} =\mathrm{2} \\ $$
Commented by mathdanisur last updated on 13/Aug/21

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Ser} \\ $$
Commented by mathdanisur last updated on 13/Aug/21
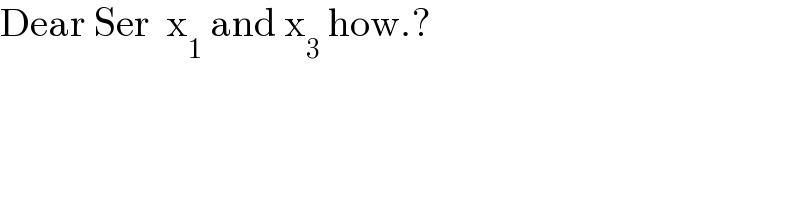
$$\mathrm{Dear}\:\mathrm{Ser}\:\:\mathrm{x}_{\mathrm{1}} \:\mathrm{and}\:\mathrm{x}_{\mathrm{3}} \:\mathrm{how}.? \\ $$
Answered by MJS_new last updated on 13/Aug/21
![7(√(4x^2 +5x−1))−14(√(x^2 −3x+3))=17x−13 squaring & transforming 2 times [(√a)−(√b)=c ⇒ a+b−2(√(ab))=c^2 ⇒ (a+b−c^2 )^2 =4ab] leads to x^4 −((17018)/(8415))x^3 −((15979)/(9537))x^2 +((68692)/(15895))x−((252148)/(143055))=0 trying factors of the constant we find ((252148)/(143055))=((2^2 ×13^2 ×373)/(3^2 ×5×11×17^2 )) (x+((2×373)/(3^2 ×5×11)))(x−((13)/(17)))^2 (x−2)=0](https://www.tinkutara.com/question/Q150541.png)
$$\mathrm{7}\sqrt{\mathrm{4}{x}^{\mathrm{2}} +\mathrm{5}{x}−\mathrm{1}}−\mathrm{14}\sqrt{{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}}=\mathrm{17}{x}−\mathrm{13} \\ $$$$\mathrm{squaring}\:\&\:\mathrm{transforming}\:\mathrm{2}\:\mathrm{times} \\ $$$$\:\:\:\:\:\left[\sqrt{{a}}−\sqrt{{b}}={c}\:\Rightarrow\:{a}+{b}−\mathrm{2}\sqrt{{ab}}={c}^{\mathrm{2}} \:\Rightarrow\:\left({a}+{b}−{c}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{4}{ab}\right] \\ $$$$\mathrm{leads}\:\mathrm{to} \\ $$$${x}^{\mathrm{4}} −\frac{\mathrm{17018}}{\mathrm{8415}}{x}^{\mathrm{3}} −\frac{\mathrm{15979}}{\mathrm{9537}}{x}^{\mathrm{2}} +\frac{\mathrm{68692}}{\mathrm{15895}}{x}−\frac{\mathrm{252148}}{\mathrm{143055}}=\mathrm{0} \\ $$$$\mathrm{trying}\:\mathrm{factors}\:\mathrm{of}\:\mathrm{the}\:\mathrm{constant}\:\mathrm{we}\:\mathrm{find} \\ $$$$\frac{\mathrm{252148}}{\mathrm{143055}}=\frac{\mathrm{2}^{\mathrm{2}} ×\mathrm{13}^{\mathrm{2}} ×\mathrm{373}}{\mathrm{3}^{\mathrm{2}} ×\mathrm{5}×\mathrm{11}×\mathrm{17}^{\mathrm{2}} } \\ $$$$\left({x}+\frac{\mathrm{2}×\mathrm{373}}{\mathrm{3}^{\mathrm{2}} ×\mathrm{5}×\mathrm{11}}\right)\left({x}−\frac{\mathrm{13}}{\mathrm{17}}\right)^{\mathrm{2}} \left({x}−\mathrm{2}\right)=\mathrm{0} \\ $$
Commented by mathdanisur last updated on 13/Aug/21

$$\mathrm{Thank}\:\mathrm{You}\:\boldsymbol{\mathrm{S}}\mathrm{er} \\ $$
