Question Number 150517 by ajfour last updated on 13/Aug/21
Commented by ajfour last updated on 13/Aug/21

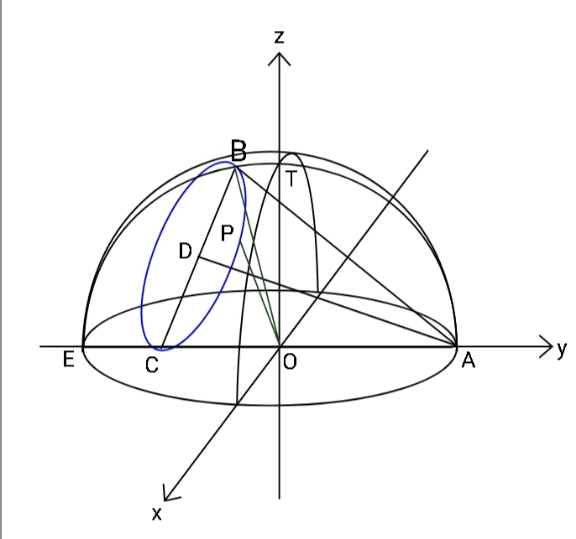
$${Cannot}\:{OP}\:{be}\:{a}\:{bit}\:{greater} \\ $$$${than}\:{OB}={R}\:\left({radius}\:{of}\:{hemi}-\right. \\ $$$$\left.{sphere}\right)?\:{If}\:{yes}\:{then}\:{for}\:{what} \\ $$$${range}\:{of}\:{semi}-{vertical}\:\angle\:\theta \\ $$$${of}\:{cone}\:\left({right}\right),\:{is}\:{that}\:{so}? \\ $$
Commented by ajfour last updated on 13/Aug/21

$$\mathcal{THANKS}\:\:\:\mathcal{S}{i}\mathcal{R}.\:{very}\:{convincing}! \\ $$
Commented by mr W last updated on 13/Aug/21

$${the}\:{circle}\:{with}\:{radius}\:{DB}\:\left(={DP}\right) \\ $$$${is}\:{always}\:{smaller}\:{than}\:{the} \\ $$$${cross}−{section}\:{circle}\:{between}\:{the} \\ $$$${sphere}\:{and}\:{the}\:{plane}\:{in}\:{which}\:{the} \\ $$$${circle}\:{with}\:{radius}\:{DB}\:{lies}.\:{than}\:{means} \\ $$$${no}\:{point}\:{on}\:{the}\:{circle}\:{with}\:{radius} \\ $$$${DB}\:{lies}\:{outside}\:{the}\:{sphere}.\:{i}.{e}.\:{P} \\ $$$${can}\:{never}\:{lie}\:{outside}\:{the}\:{sphere},\:{or} \\ $$$${OP}\leqslant{R}. \\ $$
Commented by mr W last updated on 13/Aug/21

Commented by mr W last updated on 13/Aug/21

$${blue}\:{shaded}\:{circle}\:{and}\:{red}\:{circle}\:{are} \\ $$$${in}\:{the}\:{same}\:{plane}.\:{red}\:{circle}\:{is}\:{on}\:{the} \\ $$$${sphere}.\:{since}\:{blue}\:{circle}\:{is}\:{inside}\:{the} \\ $$$${red}\:{circle}.\:{points}\:{on}\:{blue}\:{circle}\:{can} \\ $$$${never}\:{exceed}\:{the}\:{sphere}.\:\Rightarrow{OP}\leqslant{R}. \\ $$
Commented by mr W last updated on 13/Aug/21

