Question Number 150601 by mathdanisur last updated on 13/Aug/21

Answered by Olaf_Thorendsen last updated on 13/Aug/21
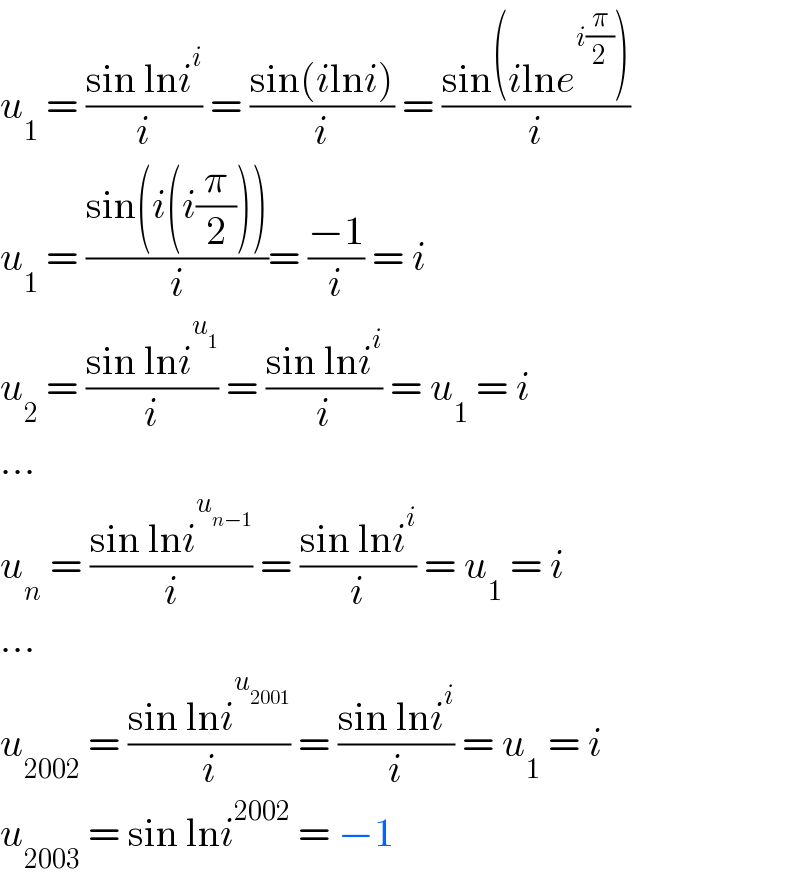
$${u}_{\mathrm{1}} \:=\:\frac{\mathrm{sin}\:\mathrm{ln}{i}^{{i}} }{{i}}\:=\:\frac{\mathrm{sin}\left({i}\mathrm{ln}{i}\right)}{{i}}\:=\:\frac{\mathrm{sin}\left({i}\mathrm{ln}{e}^{{i}\frac{\pi}{\mathrm{2}}} \right)}{{i}} \\ $$$${u}_{\mathrm{1}} \:=\:\frac{\mathrm{sin}\left({i}\left({i}\frac{\pi}{\mathrm{2}}\right)\right)}{{i}}=\:\frac{−\mathrm{1}}{{i}}\:=\:{i} \\ $$$${u}_{\mathrm{2}} \:=\:\frac{\mathrm{sin}\:\mathrm{ln}{i}^{{u}_{\mathrm{1}} } }{{i}}\:=\:\frac{\mathrm{sin}\:\mathrm{ln}{i}^{{i}} }{{i}}\:=\:{u}_{\mathrm{1}} \:=\:{i} \\ $$$$… \\ $$$${u}_{{n}} \:=\:\frac{\mathrm{sin}\:\mathrm{ln}{i}^{{u}_{{n}−\mathrm{1}} } }{{i}}\:=\:\frac{\mathrm{sin}\:\mathrm{ln}{i}^{{i}} }{{i}}\:=\:{u}_{\mathrm{1}} \:=\:{i} \\ $$$$… \\ $$$${u}_{\mathrm{2002}} \:=\:\frac{\mathrm{sin}\:\mathrm{ln}{i}^{{u}_{\mathrm{2001}} } }{{i}}\:=\:\frac{\mathrm{sin}\:\mathrm{ln}{i}^{{i}} }{{i}}\:=\:{u}_{\mathrm{1}} \:=\:{i} \\ $$$${u}_{\mathrm{2003}} \:=\:\mathrm{sin}\:\mathrm{ln}{i}^{\mathrm{2002}} \:=\:−\mathrm{1} \\ $$
Commented by mathdanisur last updated on 14/Aug/21
$$\mathrm{Thank}\:\mathrm{You}\:\mathrm{Ser}\:\mathrm{cool} \\ $$
