Question Number 150628 by aupo14 last updated on 14/Aug/21
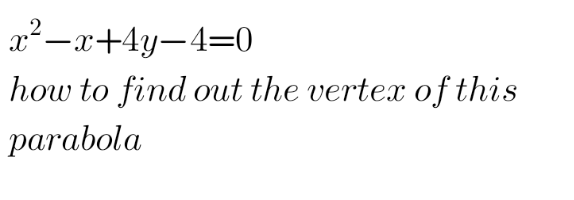
Answered by som(math1967) last updated on 14/Aug/21
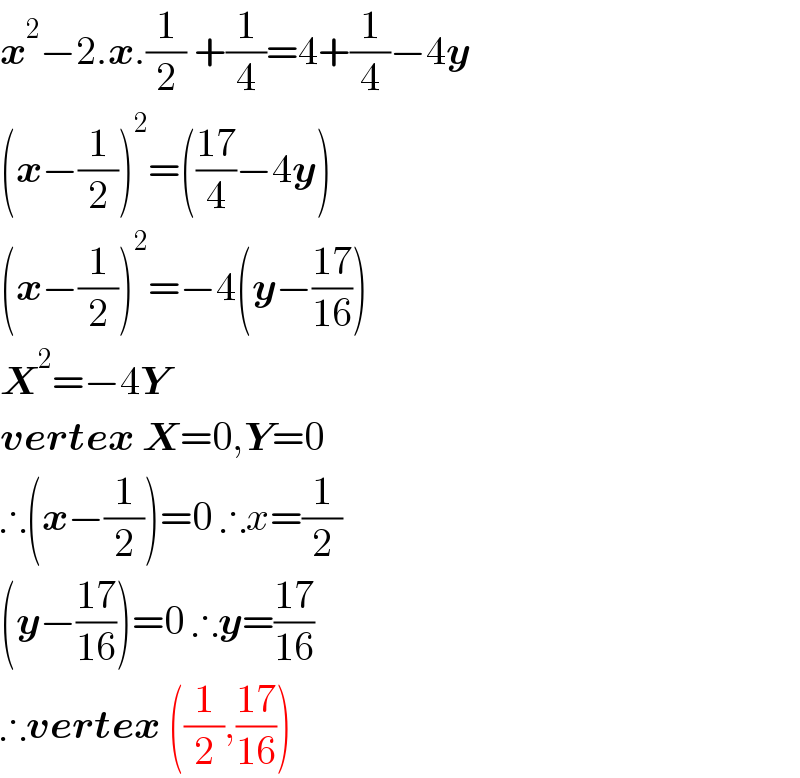
$$\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{2}.\boldsymbol{{x}}.\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{4}+\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{4}\boldsymbol{{y}} \\ $$$$\left(\boldsymbol{{x}}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} =\left(\frac{\mathrm{17}}{\mathrm{4}}−\mathrm{4}\boldsymbol{{y}}\right) \\ $$$$\left(\boldsymbol{{x}}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} =−\mathrm{4}\left(\boldsymbol{{y}}−\frac{\mathrm{17}}{\mathrm{16}}\right) \\ $$$$\boldsymbol{{X}}^{\mathrm{2}} =−\mathrm{4}\boldsymbol{{Y}} \\ $$$$\boldsymbol{{vertex}}\:\boldsymbol{{X}}=\mathrm{0},\boldsymbol{{Y}}=\mathrm{0} \\ $$$$\therefore\left(\boldsymbol{{x}}−\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{0}\:\therefore{x}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\left(\boldsymbol{{y}}−\frac{\mathrm{17}}{\mathrm{16}}\right)=\mathrm{0}\:\therefore\boldsymbol{{y}}=\frac{\mathrm{17}}{\mathrm{16}} \\ $$$$\therefore\boldsymbol{{vertex}}\:\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{17}}{\mathrm{16}}\right) \\ $$
