Menu Close

Question-150647

Tinku Tara 0 Comments
Pin




Question Number 150647 by puissant last updated on 14/Aug/21
Answered by puissant last updated on 14/Aug/21
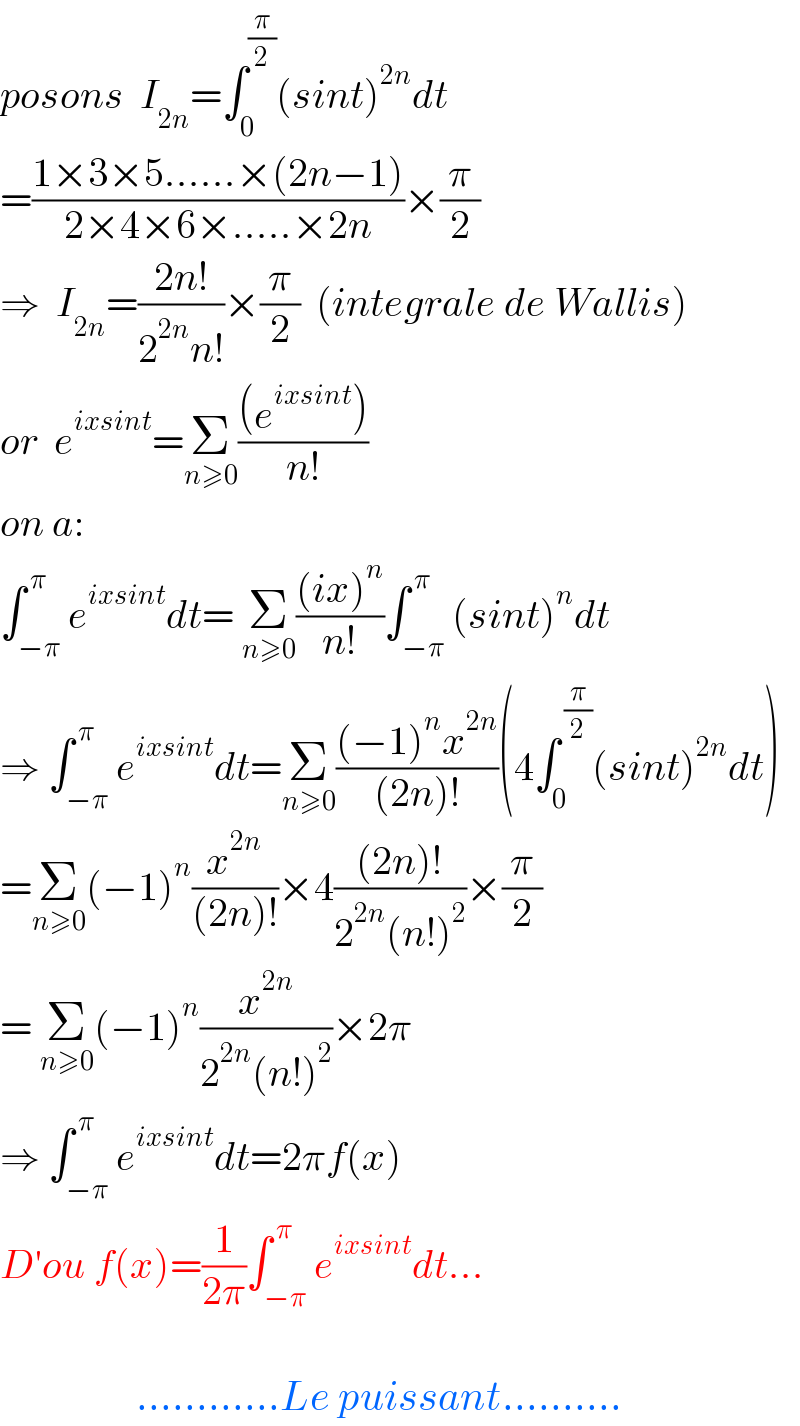
posons I_(2n) =∫_0 ^(π/2) (sint)^(2n) dt =((1×3×5......×(2n−1))/(2×4×6×.....×2n))×(π/2) ⇒ I_(2n) =((2n!)/(2^(2n) n!))×(π/2) (integrale de Wallis) or e^(ixsint) =Σ_(n≥0) (((e^(ixsint) ))/(n!)) on a: ∫_(−π) ^( π) e^(ixsint) dt= Σ_(n≥0) (((ix)^n )/(n!))∫_(−π) ^( π) (sint)^n dt ⇒ ∫_(−π) ^( π) e^(ixsint) dt=Σ_(n≥0) (((−1)^n x^(2n) )/((2n)!))(4∫_0 ^( (π/2)) (sint)^(2n) dt) =Σ_(n≥0) (−1)^n (x^(2n) /((2n)!))×4(((2n)!)/(2^(2n) (n!)^2 ))×(π/2) = Σ_(n≥0) (−1)^n (x^(2n) /(2^(2n) (n!)^2 ))×2π ⇒ ∫_(−π) ^( π) e^(ixsint) dt=2πf(x) D′ou f(x)=(1/(2π))∫_(−π) ^( π) e^(ixsint) dt... ............Le puissant..........
$${posons}\:\:{I}_{\mathrm{2}{n}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left({sint}\right)^{\mathrm{2}{n}} {dt} \\ $$$$=\frac{\mathrm{1}×\mathrm{3}×\mathrm{5}……×\left(\mathrm{2}{n}−\mathrm{1}\right)}{\mathrm{2}×\mathrm{4}×\mathrm{6}×…..×\mathrm{2}{n}}×\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow\:\:{I}_{\mathrm{2}{n}} =\frac{\mathrm{2}{n}!}{\mathrm{2}^{\mathrm{2}{n}} {n}!}×\frac{\pi}{\mathrm{2}}\:\:\left({integrale}\:{de}\:{Wallis}\right) \\ $$$${or}\:\:{e}^{{ixsint}} =\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left({e}^{{ixsint}} \right)}{{n}!} \\ $$$${on}\:{a}: \\ $$$$\int_{−\pi} ^{\:\pi} {e}^{{ixsint}} {dt}=\:\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left({ix}\right)^{{n}} }{{n}!}\int_{−\pi} ^{\:\pi} \left({sint}\right)^{{n}} {dt} \\ $$$$\Rightarrow\:\int_{−\pi} ^{\:\pi} {e}^{{ixsint}} {dt}=\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{2}{n}} }{\left(\mathrm{2}{n}\right)!}\left(\mathrm{4}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \left({sint}\right)^{\mathrm{2}{n}} {dt}\right) \\ $$$$=\underset{{n}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{{n}} \frac{{x}^{\mathrm{2}{n}} }{\left(\mathrm{2}{n}\right)!}×\mathrm{4}\frac{\left(\mathrm{2}{n}\right)!}{\mathrm{2}^{\mathrm{2}{n}} \left({n}!\right)^{\mathrm{2}} }×\frac{\pi}{\mathrm{2}} \\ $$$$=\:\underset{{n}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{{n}} \frac{{x}^{\mathrm{2}{n}} }{\mathrm{2}^{\mathrm{2}{n}} \left({n}!\right)^{\mathrm{2}} }×\mathrm{2}\pi \\ $$$$\Rightarrow\:\int_{−\pi} ^{\:\pi} {e}^{{ixsint}} {dt}=\mathrm{2}\pi{f}\left({x}\right) \\ $$$${D}'{ou}\:{f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}\pi}\int_{−\pi} ^{\:\pi} {e}^{{ixsint}} {dt}… \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…………{Le}\:{puissant}………. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *