Question Number 150697 by mathdanisur last updated on 14/Aug/21
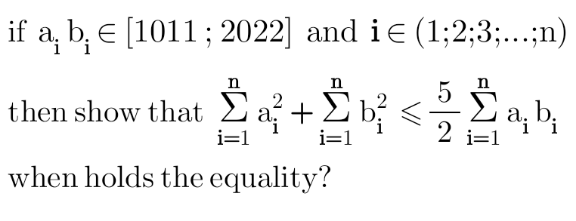
Answered by dumitrel last updated on 14/Aug/21
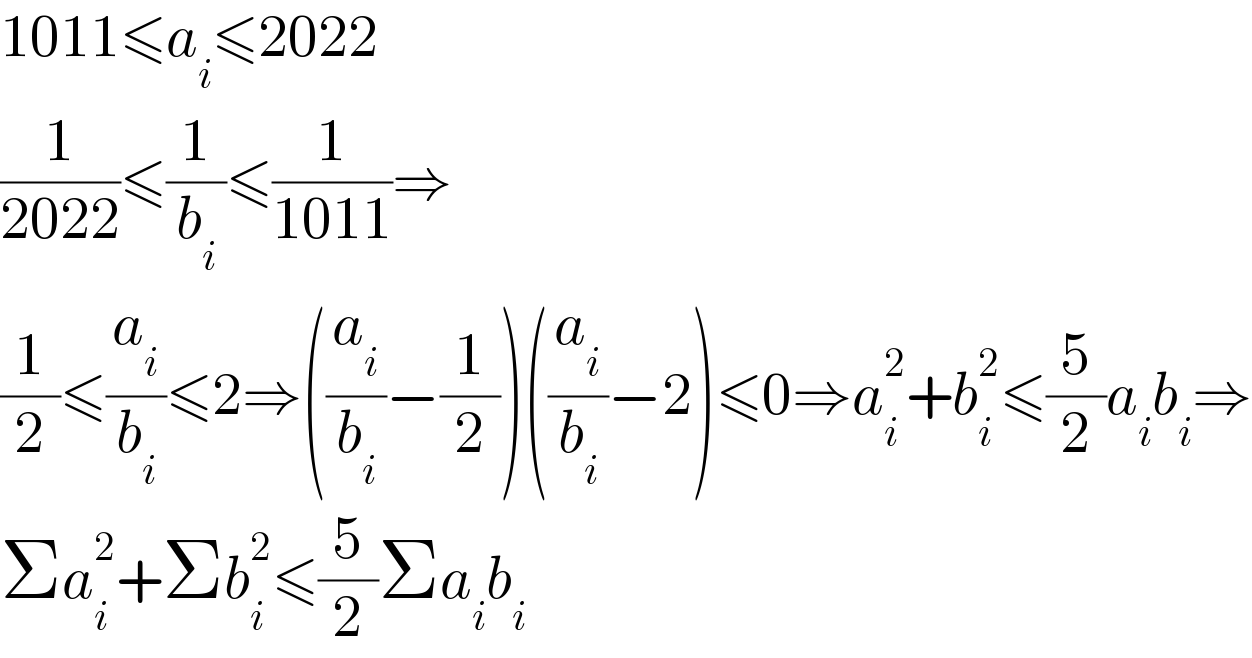
$$\mathrm{1011}\leqslant{a}_{{i}} \leqslant\mathrm{2022} \\ $$$$\frac{\mathrm{1}}{\mathrm{2022}}\leqslant\frac{\mathrm{1}}{{b}_{{i}} }\leqslant\frac{\mathrm{1}}{\mathrm{1011}}\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\leqslant\frac{{a}_{{i}} }{{b}_{{i}} }\leqslant\mathrm{2}\Rightarrow\left(\frac{{a}_{{i}} }{{b}_{{i}} }−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\frac{{a}_{{i}} }{{b}_{{i}} }−\mathrm{2}\right)\leqslant\mathrm{0}\Rightarrow{a}_{{i}} ^{\mathrm{2}} +{b}_{{i}} ^{\mathrm{2}} \leqslant\frac{\mathrm{5}}{\mathrm{2}}{a}_{{i}} {b}_{{i}} \Rightarrow \\ $$$$\Sigma{a}_{{i}} ^{\mathrm{2}} +\Sigma{b}_{{i}} ^{\mathrm{2}} \leqslant\frac{\mathrm{5}}{\mathrm{2}}\Sigma{a}_{{i}} {b}_{{i}} \\ $$
Commented by mathdanisur last updated on 14/Aug/21
$$\mathrm{Cool}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{thank}\:\mathrm{you} \\ $$
