Menu Close

Question-150838

Tinku Tara 0 Comments
Pin




Question Number 150838 by mathdanisur last updated on 15/Aug/21
Answered by amin96 last updated on 15/Aug/21
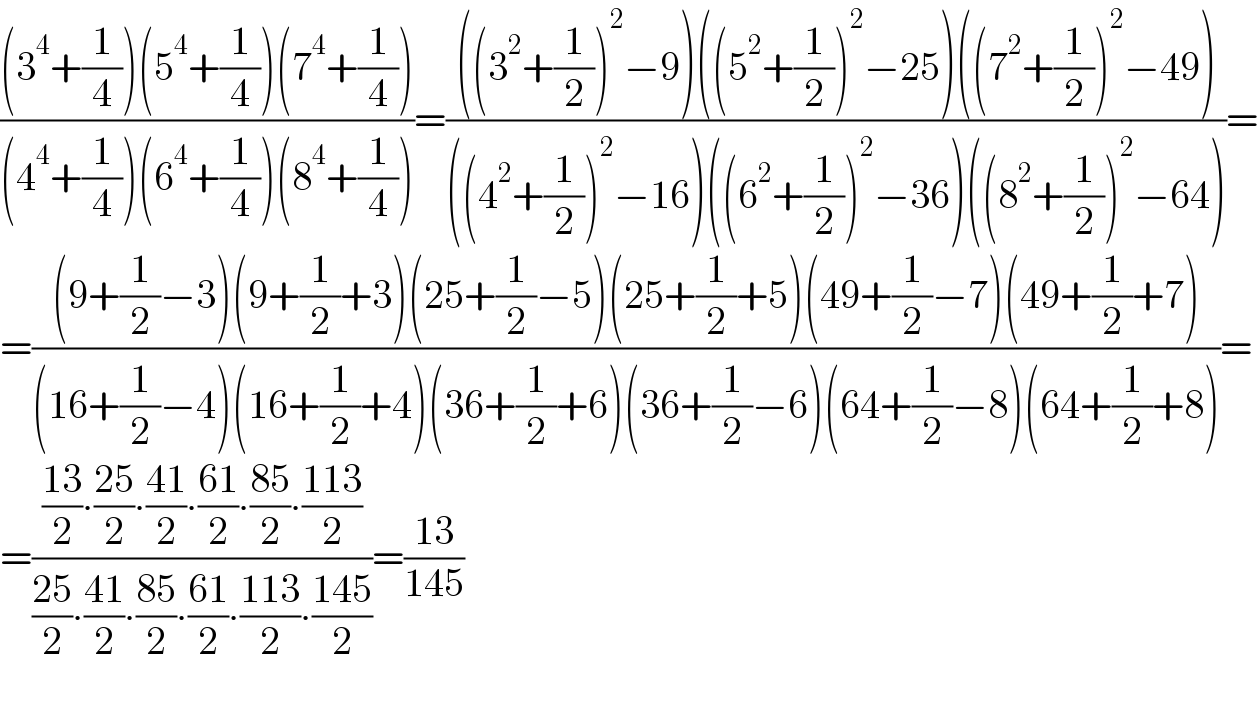
(((3^4 +(1/4))(5^4 +(1/4))(7^4 +(1/4)))/((4^4 +(1/4))(6^4 +(1/4))(8^4 +(1/4))))=((((3^2 +(1/2))^2 −9)((5^2 +(1/2))^2 −25)((7^2 +(1/2))^2 −49))/(((4^2 +(1/2))^2 −16)((6^2 +(1/2))^2 −36)((8^2 +(1/2))^2 −64)))= =(((9+(1/2)−3)(9+(1/2)+3)(25+(1/2)−5)(25+(1/2)+5)(49+(1/2)−7)(49+(1/2)+7))/((16+(1/2)−4)(16+(1/2)+4)(36+(1/2)+6)(36+(1/2)−6)(64+(1/2)−8)(64+(1/2)+8)))= =((((13)/2)∙((25)/2)∙((41)/2)∙((61)/2)∙((85)/2)∙((113)/2))/(((25)/2)∙((41)/2)∙((85)/2)∙((61)/2)∙((113)/2)∙((145)/2)))=((13)/(145))
$$\frac{\left(\mathrm{3}^{\mathrm{4}} +\frac{\mathrm{1}}{\mathrm{4}}\right)\left(\mathrm{5}^{\mathrm{4}} +\frac{\mathrm{1}}{\mathrm{4}}\right)\left(\mathrm{7}^{\mathrm{4}} +\frac{\mathrm{1}}{\mathrm{4}}\right)}{\left(\mathrm{4}^{\mathrm{4}} +\frac{\mathrm{1}}{\mathrm{4}}\right)\left(\mathrm{6}^{\mathrm{4}} +\frac{\mathrm{1}}{\mathrm{4}}\right)\left(\mathrm{8}^{\mathrm{4}} +\frac{\mathrm{1}}{\mathrm{4}}\right)}=\frac{\left(\left(\mathrm{3}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{9}\right)\left(\left(\mathrm{5}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{25}\right)\left(\left(\mathrm{7}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{49}\right)}{\left(\left(\mathrm{4}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{16}\right)\left(\left(\mathrm{6}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{36}\right)\left(\left(\mathrm{8}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{64}\right)}= \\ $$$$=\frac{\left(\mathrm{9}+\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{3}\right)\left(\mathrm{9}+\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{3}\right)\left(\mathrm{25}+\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{5}\right)\left(\mathrm{25}+\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{5}\right)\left(\mathrm{49}+\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{7}\right)\left(\mathrm{49}+\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{7}\right)}{\left(\mathrm{16}+\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{4}\right)\left(\mathrm{16}+\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{4}\right)\left(\mathrm{36}+\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{6}\right)\left(\mathrm{36}+\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{6}\right)\left(\mathrm{64}+\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{8}\right)\left(\mathrm{64}+\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{8}\right)}= \\ $$$$=\frac{\frac{\mathrm{13}}{\mathrm{2}}\centerdot\frac{\mathrm{25}}{\mathrm{2}}\centerdot\frac{\mathrm{41}}{\mathrm{2}}\centerdot\frac{\mathrm{61}}{\mathrm{2}}\centerdot\frac{\mathrm{85}}{\mathrm{2}}\centerdot\frac{\mathrm{113}}{\mathrm{2}}}{\frac{\mathrm{25}}{\mathrm{2}}\centerdot\frac{\mathrm{41}}{\mathrm{2}}\centerdot\frac{\mathrm{85}}{\mathrm{2}}\centerdot\frac{\mathrm{61}}{\mathrm{2}}\centerdot\frac{\mathrm{113}}{\mathrm{2}}\centerdot\frac{\mathrm{145}}{\mathrm{2}}}=\frac{\mathrm{13}}{\mathrm{145}} \\ $$$$ \\ $$
Commented by mathdanisur last updated on 15/Aug/21
Ser thank you
$$\mathrm{Ser}\:\mathrm{thank}\:\mathrm{you} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *