Question Number 150870 by liberty last updated on 16/Aug/21

Commented by mnjuly1970 last updated on 16/Aug/21

$$\:\:{pls}\:\:{solve}\:{it}… \\ $$
Answered by tabata last updated on 16/Aug/21
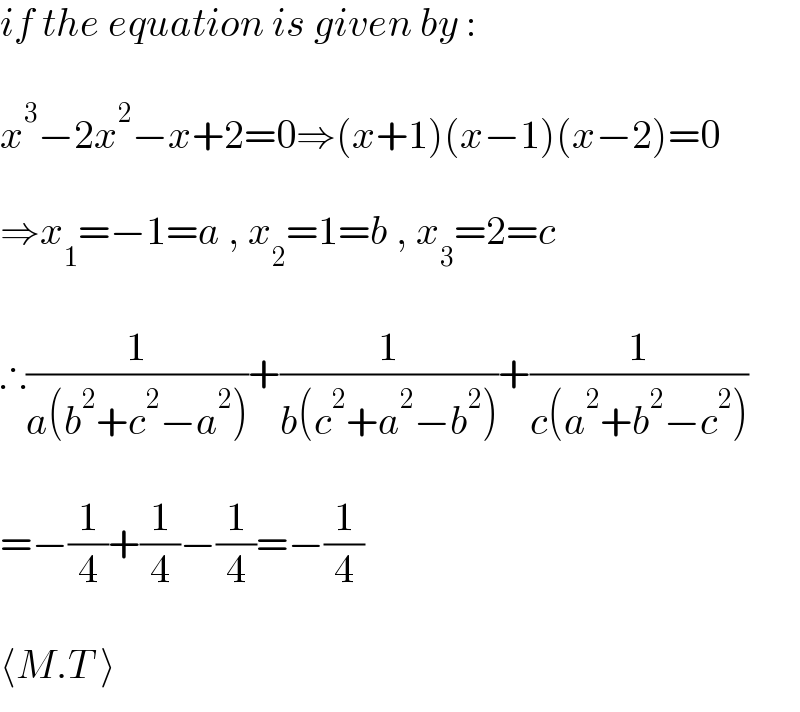
$${if}\:{the}\:{equation}\:{is}\:{given}\:{by}\:: \\ $$$$ \\ $$$${x}^{\mathrm{3}} −\mathrm{2}{x}^{\mathrm{2}} −{x}+\mathrm{2}=\mathrm{0}\Rightarrow\left({x}+\mathrm{1}\right)\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)=\mathrm{0} \\ $$$$ \\ $$$$\Rightarrow{x}_{\mathrm{1}} =−\mathrm{1}={a}\:,\:{x}_{\mathrm{2}} =\mathrm{1}={b}\:,\:{x}_{\mathrm{3}} =\mathrm{2}={c} \\ $$$$ \\ $$$$\therefore\frac{\mathrm{1}}{{a}\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)}+\frac{\mathrm{1}}{{b}\left({c}^{\mathrm{2}} +{a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)}+\frac{\mathrm{1}}{{c}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)} \\ $$$$ \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{4}}=−\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$ \\ $$$$\langle{M}.{T}\:\rangle \\ $$
