Question Number 150887 by mathdanisur last updated on 16/Aug/21

Commented by dumitrel last updated on 16/Aug/21

$${a}\leqslant{b}\leqslant{c}\leqslant{d}\Rightarrow\left({a}+{b}+{c}+{d}\right)^{\mathrm{2}} \geqslant\mathrm{8}\left({ac}+{bd}\right) \\ $$
Commented by mathdanisur last updated on 16/Aug/21
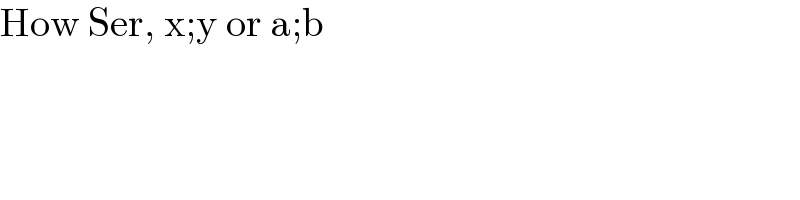
$$\mathrm{How}\:\mathrm{Ser},\:\mathrm{x};\mathrm{y}\:\mathrm{or}\:\mathrm{a};\mathrm{b} \\ $$
Commented by dumitrel last updated on 16/Aug/21

$${a}={m}_{{h}} ;\:{b}={m}_{{g}} ;\:{c}={m}_{{a}} ;{d}={m}_{{p}} \\ $$$$ \\ $$
Commented by mathdanisur last updated on 16/Aug/21

$$\mathrm{Dear}\:\mathrm{Ser},\:\mathrm{l}\:\mathrm{did}\:\mathrm{not}\:\mathrm{understand} \\ $$
Answered by dumitrel last updated on 16/Aug/21

$$\Leftrightarrow\left(\frac{{m}_{{h}} }{\mathrm{2}}+\frac{{m}_{{g}} }{\mathrm{2}}+\frac{{m}_{{a}} }{\mathrm{2}}+\frac{{m}_{{p}} }{\mathrm{2}}\right)^{\mathrm{2}} \geqslant\mathrm{2}\centerdot\frac{\mathrm{2}{xy}}{{x}+{y}}\centerdot\frac{{x}+{y}}{\mathrm{2}}+\mathrm{2}\sqrt{{xy}}\centerdot\sqrt{\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{\mathrm{2}}}\Leftrightarrow \\ $$$$\left({m}_{{h}} +{m}_{{g}} +{m}_{{a}} +{m}_{{p}} \right)^{\mathrm{2}} \geqslant\mathrm{8}\left({m}_{{h}} {m}_{{a}} +{m}_{{g}} {m}_{{p}} \right) \\ $$$${f}\left({x}\right)=\mathrm{2}{x}^{\mathrm{2}} +{x}\left({m}_{{h}} +{m}_{{g}} +{m}_{{a}} +{m}_{{p}} \right)+{m}_{{h}} {m}_{{a}} +{m}_{{g}} {m}_{{p}} \\ $$$$\Rightarrow{f}\left({x}\right)=\left({x}+{m}_{{h}} \right)\left({x}+{m}_{{a}} \right)+\left({x}+{m}_{{g}} \right)\left({x}+{m}_{{p}} \right) \\ $$$${f}\left({m}_{{h}} \right)=\left(−{m}_{{h}} +{m}_{{g}} \right)\left(−{m}_{{h}} +{m}_{{p}} \right)\geqslant\mathrm{0} \\ $$$${f}\left(−{m}_{{a}} \right)=\left(−{m}_{{a}} +{m}_{{g}} \right)\left(−{m}_{{a}} +{m}_{{p}} \right)\leqslant\mathrm{0}\Rightarrow\bigtriangleup_{{f}} \geqslant\mathrm{0}\Rightarrow \\ $$$$\left({m}_{{h}} +{m}_{{g}} +{m}_{{a}} +{m}_{{p}} \right)^{\mathrm{2}} \geqslant\mathrm{8}\left({m}_{{h}} {m}_{{a}} +{m}_{{g}} {m}_{{p}} \right) \\ $$$$ \\ $$
Commented by mathdanisur last updated on 16/Aug/21

$$\mathrm{Cool}\:\boldsymbol{\mathrm{S}}\mathrm{er}\:\mathrm{Thank}\:\mathrm{You} \\ $$
