Question Number 150895 by tabata last updated on 16/Aug/21
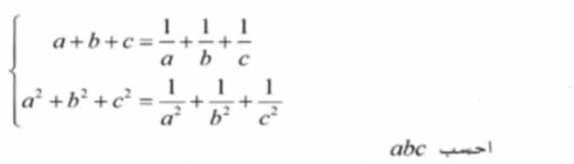
Commented by tabata last updated on 16/Aug/21

$${find}\:\left({a}.{b}.{c}\right) \\ $$
Answered by amin96 last updated on 16/Aug/21
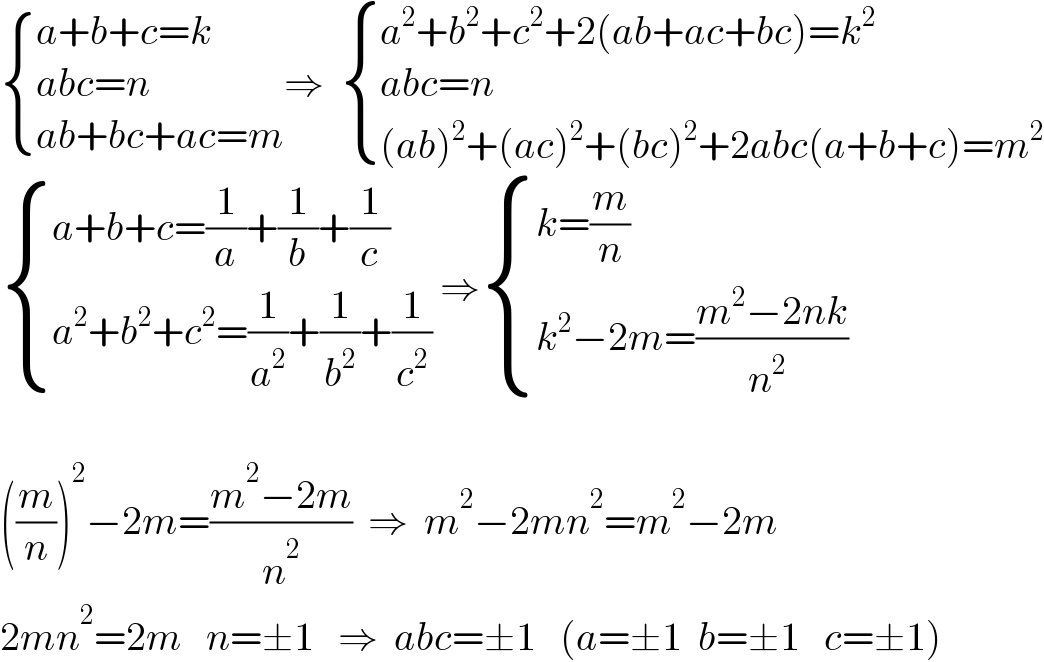
$$\begin{cases}{{a}+{b}+{c}={k}}\\{{abc}={n}}\\{{ab}+{bc}+{ac}={m}}\end{cases}\Rightarrow\:\:\begin{cases}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\mathrm{2}\left({ab}+{ac}+{bc}\right)={k}^{\mathrm{2}} }\\{{abc}={n}}\\{\left({ab}\right)^{\mathrm{2}} +\left({ac}\right)^{\mathrm{2}} +\left({bc}\right)^{\mathrm{2}} +\mathrm{2}{abc}\left({a}+{b}+{c}\right)={m}^{\mathrm{2}} }\end{cases} \\ $$$$\begin{cases}{{a}+{b}+{c}=\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}}\\{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} =\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }+\frac{\mathrm{1}}{{c}^{\mathrm{2}} }}\end{cases}\:\Rightarrow\begin{cases}{{k}=\frac{{m}}{{n}}}\\{{k}^{\mathrm{2}} −\mathrm{2}{m}=\frac{{m}^{\mathrm{2}} −\mathrm{2}{nk}}{{n}^{\mathrm{2}\:\:} }}\end{cases} \\ $$$$ \\ $$$$\left(\frac{{m}}{{n}}\right)^{\mathrm{2}} −\mathrm{2}{m}=\frac{{m}^{\mathrm{2}} −\mathrm{2}{m}}{{n}^{\mathrm{2}} }\:\:\Rightarrow\:\:{m}^{\mathrm{2}} −\mathrm{2}{mn}^{\mathrm{2}} ={m}^{\mathrm{2}} −\mathrm{2}{m} \\ $$$$\mathrm{2}{mn}^{\mathrm{2}} =\mathrm{2}{m}\:\:\:{n}=\pm\mathrm{1}\:\:\:\Rightarrow\:\:{abc}=\pm\mathrm{1}\:\:\:\left({a}=\pm\mathrm{1}\:\:{b}=\pm\mathrm{1}\:\:\:{c}=\pm\mathrm{1}\right) \\ $$
Commented by Rasheed.Sindhi last updated on 16/Aug/21

$$\mathcal{V}.\:\mathcal{N}{ice}! \\ $$
