Question Number 150918 by mathdanisur last updated on 16/Aug/21

Commented by puissant last updated on 16/Aug/21
![= [((Σ_(k=0) ^(1995) 2^k )/(1997))] = (1/(1997))(((1−2^(1996) )/(1−2))) =(1/(1997))(2^(1996) −1) =((2^(1996) −1)/(1997)) ★](https://www.tinkutara.com/question/Q150937.png)
$$=\:\left[\frac{\underset{{k}=\mathrm{0}} {\overset{\mathrm{1995}} {\sum}}\mathrm{2}^{{k}} }{\mathrm{1997}}\right]\: \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{1997}}\left(\frac{\mathrm{1}−\mathrm{2}^{\mathrm{1996}} }{\mathrm{1}−\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{1997}}\left(\mathrm{2}^{\mathrm{1996}} −\mathrm{1}\right) \\ $$$$=\frac{\mathrm{2}^{\mathrm{1996}} −\mathrm{1}}{\mathrm{1997}}\:\bigstar \\ $$
Commented by mathdanisur last updated on 16/Aug/21

$$\mathrm{is}\:\mathrm{a}\:\mathrm{full}\:\mathrm{part}\:\mathrm{purchase}\:\mathrm{operation} \\ $$
Answered by nimnim last updated on 16/Aug/21
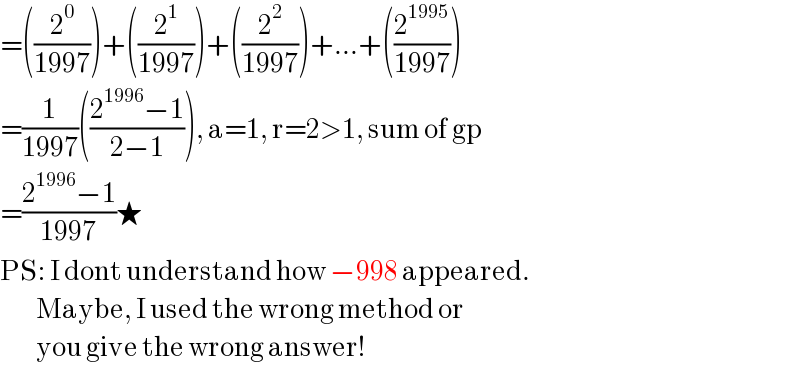
$$=\left(\frac{\mathrm{2}^{\mathrm{0}} }{\mathrm{1997}}\right)+\left(\frac{\mathrm{2}^{\mathrm{1}} }{\mathrm{1997}}\right)+\left(\frac{\mathrm{2}^{\mathrm{2}} }{\mathrm{1997}}\right)+…+\left(\frac{\mathrm{2}^{\mathrm{1995}} }{\mathrm{1997}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{1997}}\left(\frac{\mathrm{2}^{\mathrm{1996}} −\mathrm{1}}{\mathrm{2}−\mathrm{1}}\right),\:\mathrm{a}=\mathrm{1},\:\mathrm{r}=\mathrm{2}>\mathrm{1},\:\mathrm{sum}\:\mathrm{of}\:\mathrm{gp} \\ $$$$=\frac{\mathrm{2}^{\mathrm{1996}} −\mathrm{1}}{\mathrm{1997}}\bigstar \\ $$$$\mathrm{PS}:\:\mathrm{I}\:\mathrm{dont}\:\mathrm{understand}\:\mathrm{how}\:−\mathrm{998}\:\mathrm{appeared}. \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{Maybe},\:\mathrm{I}\:\mathrm{used}\:\mathrm{the}\:\mathrm{wrong}\:\mathrm{method}\:\mathrm{or} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{you}\:\mathrm{give}\:\mathrm{the}\:\mathrm{wrong}\:\mathrm{answer}! \\ $$
Commented by mr W last updated on 16/Aug/21
![[x]=greatest integer equal to or less than x. [(1/(1997))]=0 [(2/(1997))]=0 ... [(2^(10) /(1997))]=0 [(2^(11) /(1997))]=1 [(2^(12) /(1997))]=2 ...](https://www.tinkutara.com/question/Q150935.png)
$$\left[{x}\right]={greatest}\:{integer}\:{equal}\:{to}\:{or}\:{less} \\ $$$${than}\:{x}. \\ $$$$\left[\frac{\mathrm{1}}{\mathrm{1997}}\right]=\mathrm{0} \\ $$$$\left[\frac{\mathrm{2}}{\mathrm{1997}}\right]=\mathrm{0} \\ $$$$… \\ $$$$\left[\frac{\mathrm{2}^{\mathrm{10}} }{\mathrm{1997}}\right]=\mathrm{0} \\ $$$$\left[\frac{\mathrm{2}^{\mathrm{11}} }{\mathrm{1997}}\right]=\mathrm{1} \\ $$$$\left[\frac{\mathrm{2}^{\mathrm{12}} }{\mathrm{1997}}\right]=\mathrm{2} \\ $$$$… \\ $$
Answered by maged last updated on 16/Aug/21

$$\frac{\mathrm{2}^{\mathrm{1996}} −\mathrm{1}}{\mathrm{1997}} \\ $$
