Question Number 150965 by EDWIN88 last updated on 17/Aug/21

Answered by john_santu last updated on 17/Aug/21
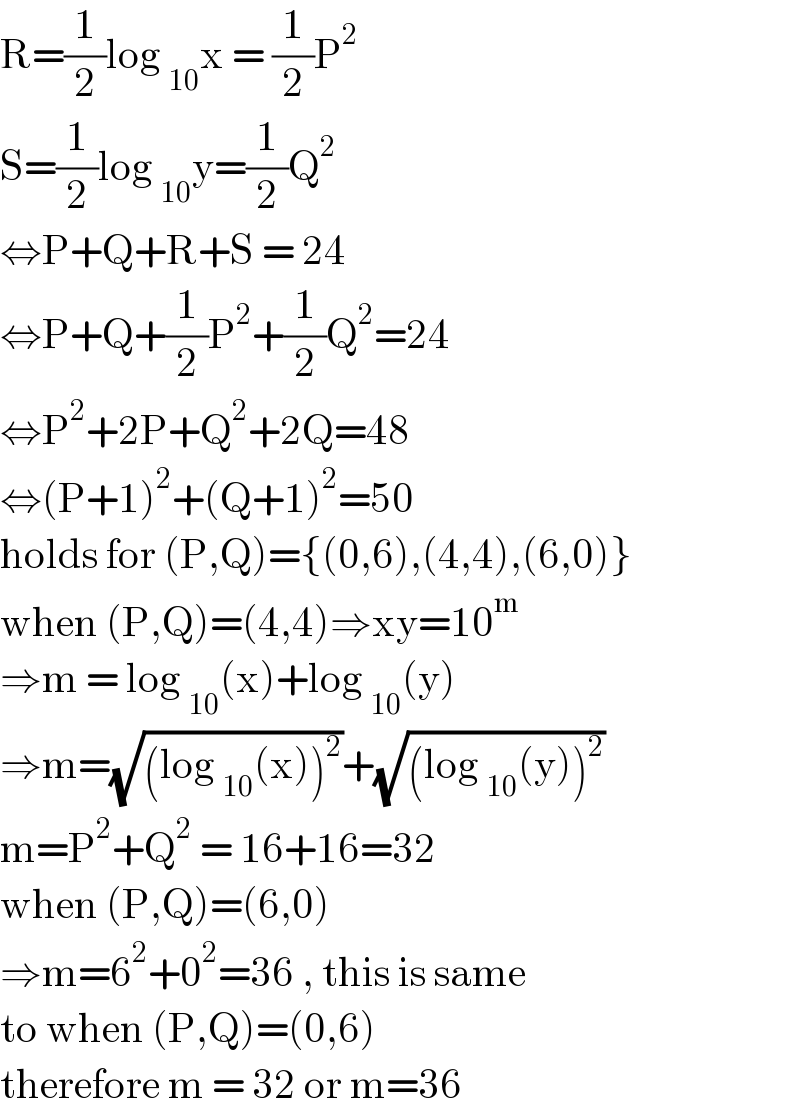
$$\mathrm{R}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\:_{\mathrm{10}} \mathrm{x}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{P}^{\mathrm{2}} \\ $$$$\mathrm{S}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\:_{\mathrm{10}} \mathrm{y}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Q}^{\mathrm{2}} \\ $$$$\Leftrightarrow\mathrm{P}+\mathrm{Q}+\mathrm{R}+\mathrm{S}\:=\:\mathrm{24}\: \\ $$$$\Leftrightarrow\mathrm{P}+\mathrm{Q}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{P}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Q}^{\mathrm{2}} =\mathrm{24} \\ $$$$\Leftrightarrow\mathrm{P}^{\mathrm{2}} +\mathrm{2P}+\mathrm{Q}^{\mathrm{2}} +\mathrm{2Q}=\mathrm{48} \\ $$$$\Leftrightarrow\left(\mathrm{P}+\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{Q}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{50} \\ $$$$\mathrm{holds}\:\mathrm{for}\:\left(\mathrm{P},\mathrm{Q}\right)=\left\{\left(\mathrm{0},\mathrm{6}\right),\left(\mathrm{4},\mathrm{4}\right),\left(\mathrm{6},\mathrm{0}\right)\right\} \\ $$$$\mathrm{when}\:\left(\mathrm{P},\mathrm{Q}\right)=\left(\mathrm{4},\mathrm{4}\right)\Rightarrow\mathrm{xy}=\mathrm{10}^{\mathrm{m}} \\ $$$$\Rightarrow\mathrm{m}\:=\:\mathrm{log}\:_{\mathrm{10}} \left(\mathrm{x}\right)+\mathrm{log}\:_{\mathrm{10}} \left(\mathrm{y}\right) \\ $$$$\Rightarrow\mathrm{m}=\sqrt{\left(\mathrm{log}\:_{\mathrm{10}} \left(\mathrm{x}\right)\right)^{\mathrm{2}} }+\sqrt{\left(\mathrm{log}\:_{\mathrm{10}} \left(\mathrm{y}\right)\right)^{\mathrm{2}} } \\ $$$$\mathrm{m}=\mathrm{P}^{\mathrm{2}} +\mathrm{Q}^{\mathrm{2}} \:=\:\mathrm{16}+\mathrm{16}=\mathrm{32} \\ $$$$\mathrm{when}\:\left(\mathrm{P},\mathrm{Q}\right)=\left(\mathrm{6},\mathrm{0}\right) \\ $$$$\Rightarrow\mathrm{m}=\mathrm{6}^{\mathrm{2}} +\mathrm{0}^{\mathrm{2}} =\mathrm{36}\:,\:\mathrm{this}\:\mathrm{is}\:\mathrm{same} \\ $$$$\mathrm{to}\:\mathrm{when}\:\left(\mathrm{P},\mathrm{Q}\right)=\left(\mathrm{0},\mathrm{6}\right) \\ $$$$\mathrm{therefore}\:\mathrm{m}\:=\:\mathrm{32}\:\mathrm{or}\:\mathrm{m}=\mathrm{36}\: \\ $$
