Question-151010

Question Number 151010 by tabata last updated on 17/Aug/21

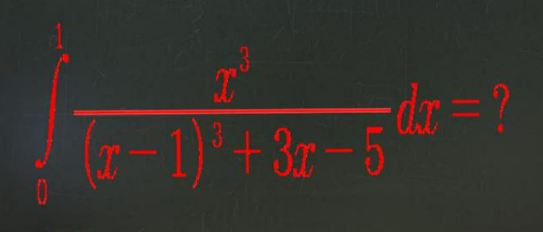
Commented by tabata last updated on 17/Aug/21

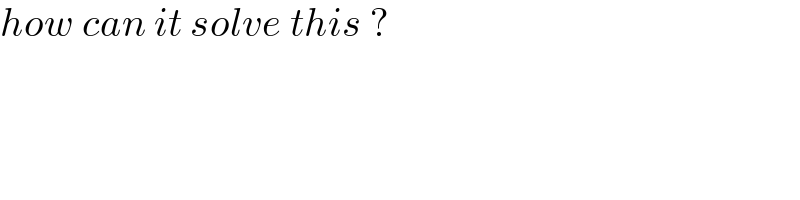
h o w c a n i t s o l v e t h i s ?

Answered by Olaf_Thorendsen last updated on 17/Aug/21

I = {\int_{0}}^{1} \frac{x^{3}}{{(x - 1)}^{3} + 3 x - 5} d x

I = {\int_{0}}^{1} \frac{x^{3}}{x^{3} - 3 x^{2} + 6 x - 6} d x

I = {\int_{0}}^{1} \frac{(x^{3} - 3 x^{2} + 6 x - 6) + (3 x^{2} - 6 x + 6)}{x^{3} - 3 x^{2} + 6 x - 6} d x

I = {\int_{0}}^{1} 1 + (\frac{3 x^{2} - 6 x + 6}{x^{3} - 3 x^{2} + 6 x - 6}) d x

I = {[x + \ln ∣ x^{3} - 3 x^{2} + 6 x - 6 ∣]}_{0}^{1}

I = 1 + \ln 2 - \ln 6

I = 1 - \ln 3

Commented by peter frank last updated on 18/Aug/21

t h a n k y o u