Menu Close

Question-151053

Tinku Tara 0 Comments
Pin




Question Number 151053 by Tawa11 last updated on 17/Aug/21
Answered by puissant last updated on 18/Aug/21
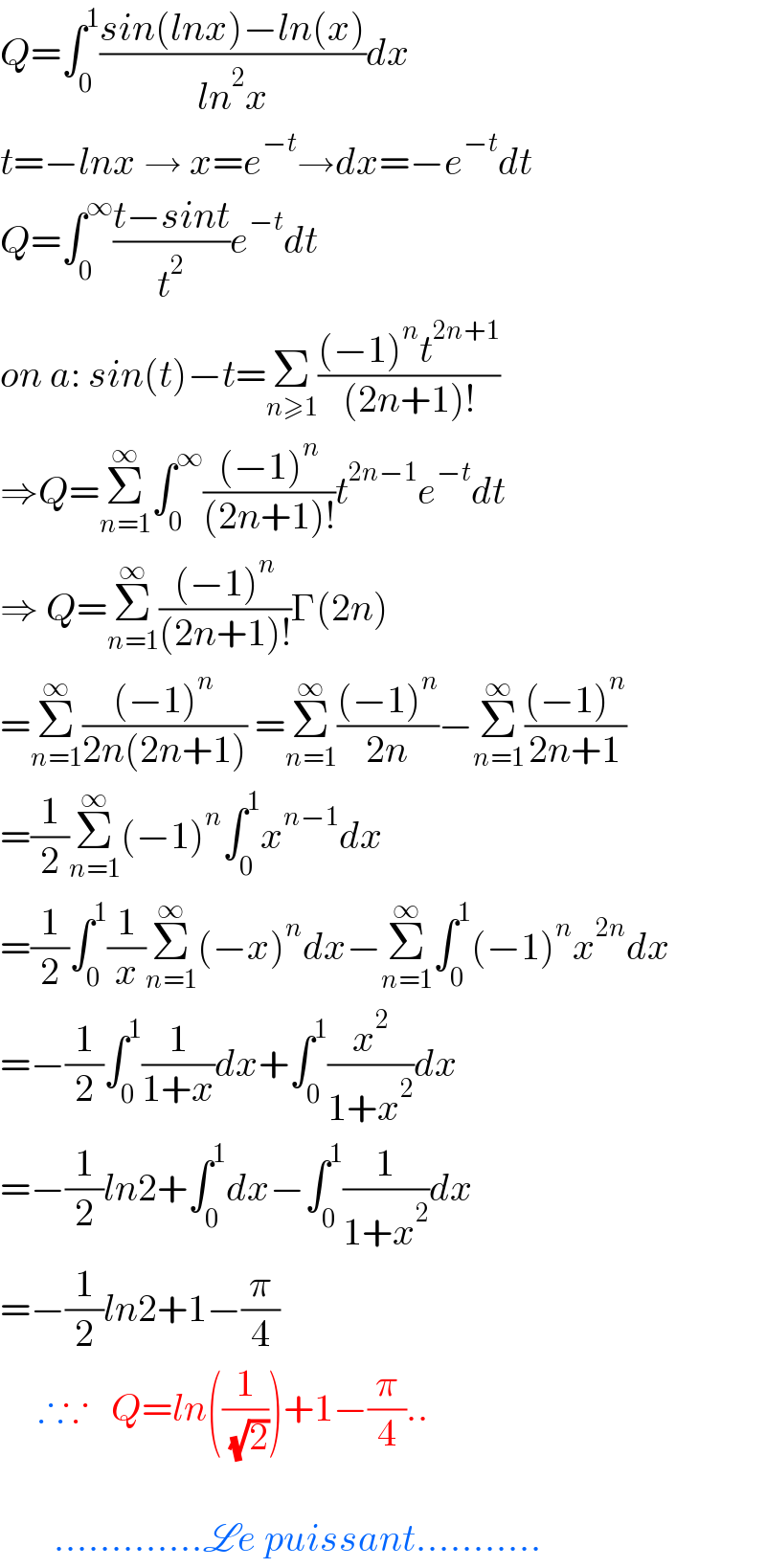
Q=∫_0 ^1 ((sin(lnx)−ln(x))/(ln^2 x))dx t=−lnx → x=e^(−t) →dx=−e^(−t) dt Q=∫_0 ^∞ ((t−sint)/t^2 )e^(−t) dt on a: sin(t)−t=Σ_(n≥1) (((−1)^n t^(2n+1) )/((2n+1)!)) ⇒Q=Σ_(n=1) ^∞ ∫_0 ^∞ (((−1)^n )/((2n+1)!))t^(2n−1) e^(−t) dt ⇒ Q=Σ_(n=1) ^∞ (((−1)^n )/((2n+1)!))Γ(2n) =Σ_(n=1) ^∞ (((−1)^n )/(2n(2n+1))) =Σ_(n=1) ^∞ (((−1)^n )/(2n))−Σ_(n=1) ^∞ (((−1)^n )/(2n+1)) =(1/2)Σ_(n=1) ^∞ (−1)^n ∫_0 ^1 x^(n−1) dx =(1/2)∫_0 ^1 (1/x)Σ_(n=1) ^∞ (−x)^n dx−Σ_(n=1) ^∞ ∫_0 ^1 (−1)^n x^(2n) dx =−(1/2)∫_0 ^1 (1/(1+x))dx+∫_0 ^1 (x^2 /(1+x^2 ))dx =−(1/2)ln2+∫_0 ^1 dx−∫_0 ^1 (1/(1+x^2 ))dx =−(1/2)ln2+1−(π/4) ∴∵ Q=ln((1/( (√2))))+1−(π/4).. .............Le puissant...........
$${Q}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{sin}\left({lnx}\right)−{ln}\left({x}\right)}{{ln}^{\mathrm{2}} {x}}{dx} \\ $$$${t}=−{lnx}\:\rightarrow\:{x}={e}^{−{t}} \rightarrow{dx}=−{e}^{−{t}} {dt} \\ $$$${Q}=\int_{\mathrm{0}} ^{\infty} \frac{{t}−{sint}}{{t}^{\mathrm{2}} }{e}^{−{t}} {dt} \\ $$$${on}\:{a}:\:{sin}\left({t}\right)−{t}=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} {t}^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!} \\ $$$$\Rightarrow{Q}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}{t}^{\mathrm{2}{n}−\mathrm{1}} {e}^{−{t}} {dt} \\ $$$$\Rightarrow\:{Q}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}\Gamma\left(\mathrm{2}{n}\right) \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}\left(\mathrm{2}{n}+\mathrm{1}\right)}\:=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}}−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}−\mathrm{1}} {dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{{x}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−{x}\right)^{{n}} {dx}−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{2}{n}} {dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+{x}}{dx}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}{ln}\mathrm{2}+\int_{\mathrm{0}} ^{\mathrm{1}} {dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}{ln}\mathrm{2}+\mathrm{1}−\frac{\pi}{\mathrm{4}} \\ $$$$\:\:\:\:\:\therefore\because\:\:\:{Q}={ln}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)+\mathrm{1}−\frac{\pi}{\mathrm{4}}.. \\ $$$$ \\ $$$$\:\:\:\:\:\:\:………….\mathscr{L}{e}\:{puissant}……….. \\ $$
Commented by Tawa11 last updated on 18/Aug/21
Thanks sir. God bless you sir.
$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *